Решебник по алгебре 8 класс Макарычев ФГОС Задание 225

 

\[\boxed{\text{225\ (225).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\frac{x + y}{y} = 3\]

\[x + y = 3y\]

\[x = 2y\]

\[\textbf{а)}\ \frac{x}{y} = \frac{2y}{y} = 2\]

\[\textbf{б)}\ \frac{y}{x + y} = \frac{y}{2y + y} = \frac{y}{3y} = \frac{1}{3}\ \]

\[\textbf{в)}\ \frac{x - y}{y} = \frac{2y - y}{y} = \frac{y}{y} = 1\]

\[\textbf{г)}\ \frac{y}{x} = \frac{y}{2y} = \frac{1}{2}\]

\[\boxed{\text{225.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же:

\[\frac{a}{b} + \frac{c}{b} = \frac{a + c}{b}.\]

Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель оставить тем же:

\[\frac{a}{b} - \frac{c}{b} = \frac{a - c}{b}.\]

Понадобятся формулы:

\[a^{2} - b^{2} = (a - b)(a + b).\]

Решение.

\[\textbf{а)}\ \frac{(y - b)^{2}}{y - b + 1} + \frac{y - b}{y - b + 1} =\]

\[= \frac{(y - b)^{2} + y - b}{y - b + 1} =\]

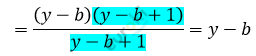
\[\textbf{б)}\ \frac{(a + x)^{2}}{a + x - 2} - \frac{2a + 2x}{a + x - 2} =\]

\[= \frac{(a + x)^{2} - 2(a + x)}{a + x - 2} =\]

\[= a + x\]

\[\textbf{в)}\ \frac{x^{2} - y^{2}}{x - y - 1} + \frac{x + y}{y - x + 1} =\]

\[= \frac{\left( x^{2} - y^{2} \right) - (x + y)}{x - y - 1} =\]

\[= x + y\]

\[\textbf{г)}\ \frac{b^{2} - 9c^{2}}{b + 3c - 2} + \frac{2(b - 3c)}{2 - b - 3c} =\]

\[= \frac{b^{2} - 9c^{2} - 2(b - 3c)}{b + 3c - 2} =\]

\[= b - 3c\]