Решебник по алгебре 8 класс Макарычев ФГОС Задание 205

 

\[\boxed{\text{205\ (205).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\frac{1}{a} + \frac{1}{b} = \frac{1}{7}\]

\[\frac{1}{a} = \frac{1^{\backslash b}}{7} - \frac{1^{\backslash 7}}{b}\]

\[\frac{1}{a} = \frac{b - 7}{7b}\]

\[a = 1\ :\frac{b - 7}{7b} = \frac{7b}{b - 7} =\]

\[= \frac{7b - 49 + 49}{b - 7} =\]

\[= \frac{7(b - 7) + 49}{b - 7} =\]

\[= \frac{7(b - 7)}{b - 7} + \frac{49}{b - 7} = 7 + \frac{49}{b - 7}.\]

\[a \in N\ \ при\ 7 + \frac{49}{b - 7} \in \text{N.}\]

\[\ \frac{49}{b - 7} \in N,\ то\ есть:\ \]

\[b - 7 = 1;7;49.\]

\[b = 14 \rightarrow \ a = 14;\]

\[b = 56 \rightarrow \ \ a = 8;\]

\[b = 8\ \rightarrow a = 56.\]

\[Ответ:(14;14),\ (8;56),\ (56;8).\]

\[\boxed{\text{205.}\text{\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]

Пояснение.

Представим дробь в виде суммы многочлена и дроби, выделив сначала в числителе квадрат разности. Разделим его на двучлен в знаменателе. Запишем дробь в виде суммы целого числа и дроби.

Решение.

\[\textbf{а)}\ \frac{m^{2} - 6m + 10}{m - 3} =\]

\[= \frac{m^{2} - 6m + 9 + 1}{m - 3} =\]

\[= \frac{(m - 3)^{2} + 1}{m - 3} =\]

\[= \frac{(m - 3)^{2}}{m - 3} + \frac{1}{m - 3} =\]

\[= m - 3 + \frac{1}{m - 3}\]

\[m \in Z;\ \ m - 3 + \frac{1}{m - 3}\ \in Z\]

\[\frac{1}{m - 3}\ \in Z\ \ m - 3 \in \left\{ - 1;1 \right\}\]

\[\frac{m^{2} - 6m + 10}{m - 3} \in \left\{ - 2;2 \right\}.\]

\[Ответ:\ - 2;2.\]

\[\textbf{б)}\ \frac{(m - 4)^{2}}{m - 2} = \frac{m^{2} - 8m + 16}{m - 2} =\]

\[= \frac{m^{2} - 4m + 4 - 4m + 12}{m - 2} =\]

\[= \frac{(m - 2)^{2} - 4m + 8 + 4}{m - 2} =\]

\[= \frac{(m - 2)^{2}}{m - 2} - \frac{4m - 8}{m - 2} + \frac{4}{m - 2} =\]

\[= m - 2 - \frac{4(m - 2)}{m - 2} + \frac{4}{m - 2} =\]

\[= m - 2 - 4 + \frac{4}{m - 2} =\]

\[= m - 6 + \frac{4}{m - 2}\]

\[m \in Z,\ \ \ m - 6 + \frac{4}{m - 2} \in Z\]

\[\frac{4}{m - 2} \in Z\]

\[Значение\ дроби\ является\ \]

\[целым\ числом\ только\ тогда,\ \]

\[когда\ знаменатель\ дроби\ \]

\[равен:\]

\[m - 2 \in \left\{ - 4;\ - 2;\ - 1;1;2;4 \right\}.\]

\[m = - 2\]

\[m = 0\]

\[m = 1\]

\[m = 3\]

\[m = 4\]

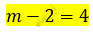
\[m = 6\]

\[\frac{(m - 4)^{2}}{m - 2} \in \left\{ - 9,\ - 8,\ 0,\ 1 \right\}\]

\[Ответ:\ - 9;\ - 8;0;1.\]