Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Макарычев ФГОС Задание 187
Задание 187
\[\boxed{\text{187\ (187).\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\(а)\frac{8}{x} = x^{2}\)
\[\left\{ \begin{matrix} y = \frac{8}{x}\text{\ \ } \\ y = x^{2} \\ \end{matrix} \right.\ \]
\[y = \frac{8}{x}\]
| \[x\] | \[1\] | \[2\] | \[4\] | \[- 1\] | \[- 2\] | \[- 4\] |
|---|---|---|---|---|---|---|
| \[y\] | \[8\] | \[4\] | \[2\] | \[- 8\] | \[- 4\] | \[- 2\] |
\[y = x^{2}\]
| \[x\] | \[- 3\] | \[- 2\] | \[- 1\] | \[0\] | \[1\] | \[2\] | \[3\] |
|---|---|---|---|---|---|---|---|
| \[y\] | \[9\] | \[4\] | \[1\] | \[0\] | \[1\] | \[4\] | \[9\] |
\[Ответ:\ \ x = 2.\]
\[\textbf{б)}\ \frac{8}{x} = x^{3}\]
\[\left\{ \begin{matrix} y = \frac{8}{x}\text{\ \ } \\ y = x^{3} \\ \end{matrix}\ \right.\ \]
\[y = \frac{8}{x}\]
| \[x\] | \[1\] | \[2\] | \[4\] | \[- 1\] | \[- 2\] | \[- 4\] |
|---|---|---|---|---|---|---|
| \[y\] | \[8\] | \[4\] | \[2\] | \[- 8\] | \[- 4\] | \[- 2\] |
\[y = x^{3}\]
| \[x\] | \[- 2\] | \[- 1\] | \[0\] | \[1\] | \[2\] |
|---|---|---|---|---|---|
| \[y\] | \[- 8\] | \[- 1\] | \[0\] | \[1\] | \[8\] |
\[Ответ:x \approx \pm 1,7.\]
\[\boxed{\text{187.\ }\text{еуроки}\text{-}\text{ответы}\text{\ }\text{на}\text{\ }\text{пятёрку}}\]
Пояснение.
Чтобы построить график обратной пропорциональности (y=k/x), нужно найти значения y, которые соответствуют некоторым положительным и отрицательным значениям x (x не равен 0). Затем отметить нужные точки в координатной плоскости и соединить их двумя плавными линиями.
Решение.
\[y = - \frac{8}{x}\]
| \[x\] | \[0\] | \[1\] | \[2\] | \[4\] | \[8\] | \[- 1\] | \[- 2\] | \[- 4\] | \[- 8\] |
|---|---|---|---|---|---|---|---|---|---|
| \[y\] | \[-\] | \[- 8\] | \[- 4\] | \[- 2\] | \[- 1\] | \[8\] | \[4\] | \[2\] | \[1\] |
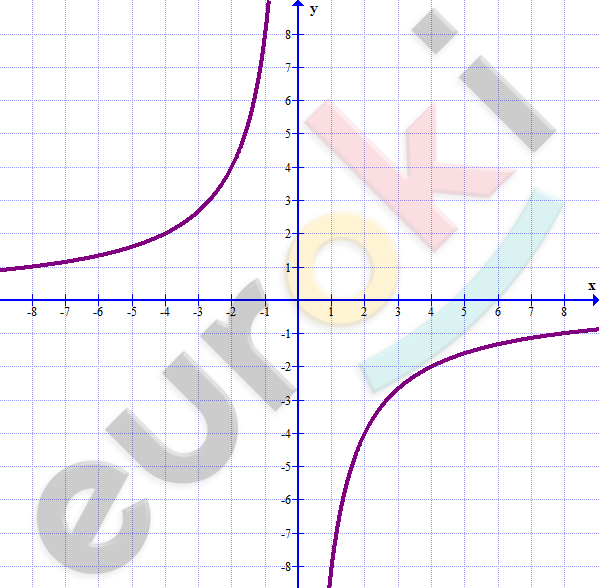
\[\textbf{а)}\ x = 4 \rightarrow y = - 2;\]
\[x = 2,5 \rightarrow y = - 3,2;\]
\[x = 1,5 \rightarrow y \approx - 5,3;\]
\[x = - 1 \rightarrow y = 8;\]
\[x = - 2,5 \rightarrow y = 3,2.\]
\[\textbf{б)}\ y = 8 \rightarrow x = - 1;\]
\(y = - 2 \rightarrow x = 4.\)
