Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 8 класс Макарычев ФГОС Вопросы к параграфу 10
Вопросы к параграфу 10
\[\boxed{\text{10.\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\boxed{\text{1.\ }}\]
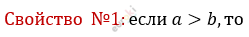
\[b < a;\]
\[если\ a < b,\ то\ \ b > a.\]
\[Доказательство:если\ разность\ \]
\[a - b > 0,\ то\ разность\ \]
\[b - a < 0\]
\[и\ наоборот.\ \]
\[Что\ и\ требовалось\ доказать.\]
\[1)\ Если\ a < b\ и\ b < c,\ то\ a < c.\]
\[Доказательство:\]
\[ пусть\ a - c < 0,\ прибавим\ \]
\[числа\ ( - b)\ и\ b \Longrightarrow\]
\[\ a - c\ = \ a - c + b - b\ = \ \]
\[= (a - b) + (b - c).\ \]
\[Так\ как\ a - b < 0,\ b - c < 0,\ \]
\[то\ (a - b) + (b - c) < 0\ и\ \]
\[a - c < 0 \Longrightarrow a < c\text{.\!}\]
\[любое\ число,\ то\ a + c < b + c.\]
\[Доказательство:\]
\[(a + c) - (b + c) =\]
\[= a + c - b - c = a - b.\ \]
\[Так\ как\ a - b < 0,\ то\]
\[\ (a + c) - (b + c) < 0 \Longrightarrow\]
\[\Longrightarrow a + c < b + c - ч.т.д.\]
\[Если\ к\ обеим\ частям\ верного\ \]
\[неравенства\ прибавить\ одно\ \]
\[и\ то\ же\ число,\ то\ получится\ \]
\[верное\ неравенство.\]
\[c > 0,\ то\ ac < bc;\]
\[если\ a < b\ \ и\ c < 0,\ то\ ac > bc.\]
\[Доказательство:ac - bc =\]
\[= c(a - b),\ так\ как\ \]
\[по\ условию\ a < b,\ то\ \]
\[a - b < 0.\ Еси\ c > 0,\ то\ \ \]
\[c(a - b) < 0\ \ и\ ac < bc.\]
\[А\ если\ c < 0,\ то\ c(a - b) > 0\ \ и\ \]
\[\text{\ \ }ac > bc \Longrightarrow что\ и\ требовалось\ \]
\[доказать.\]
\[c < d,\ то\ a + c < b + d.\]
\[Доказательство:прибавим\ \]
\[к\ обеим\ частям\ неравенство\ \]
\[a < b\ число\ c \Longrightarrow a + c < b + c.\ \]
\[А\ к\ неравенству\ c < d\ число\ \]
\[b\ \Longrightarrow c + b < d + b.\]
\[Получаем:\]
\[a + c < b + c < b + d,\ то\ \]
\[a + c < b + d \Longrightarrow ч.\ т.\ д.\]
\[c < d,\ где\ a,\ b,\ c\ и\ d -\]
\[положительные\ числа,\ то\ \]
\[ac < bd.\]
\[Доказательство:умножим\ обе\ \]
\[части\ неравенства\ \]
\[a < b\ на\ число\ c \Longrightarrow ac < bc;\]
\[умножим\ обе\ части\ \]
\[неравенства\ c < d\ на\ число\ \]
\[b \Longrightarrow bc < bd.\]
\[Получаем:ac < bc < bd,\]
\[\text{\ \ }то\ ac < bd - ч.т.д.\]
\[\boxed{\text{2.\ }}\]
\[если\ сложить\ почленно\ \]
\[верные\ неравенства\ одного\ \]
\[знака,\ то\ получится\ верное\ \]
\[неравенство\ того\ же\ знака.\]
\[Доказательство:\]
\[Если\ a\ < \ b\ и\ с\ < \ d,\ то\ \]
\[a\ + \ c\ < \ b\ + \ d.\]
\[К\ обеим\ частям\ неравенства\ \]
\[a < b\ прибавим\ число\ с\ и\ \]
\[получим\ верное\ неравенство\ \]
\[a\ + \ c\ < \ b\ + \ c.\ \]
\[Аналогично,\ к\ обеим\ частям\ \]
\[неравенства\ с\ < \ d\ прибавим\ \]
\[число\ b\ и\ получим\ верное\ \]
\[неравенство\ b\ + \ c\ < \ b\ + \ d.\ \]
\[Сравнивая\ два\ неравенства\ \]
\[a\ + \ c\ < \ b\ + \ c\ и\ \]
\[b\ + \ c\ < \ b\ + \ d,\ получаем\ \]
\[неравенство\ a\ + \ с\ < \ b\ + \ d.\]
\[если\ почленно\ перемножить\ \]
\[верные\ неравенства\ одного\ \]
\[знака,\ левые\ и\ правые\ части\ \]
\[которых\ положительные\ \]
\[числа,\ то\ получим\ верное\ \]
\[неравенство.\]
\[Если\ a < b,\ c < d,\ где\ a\ b,\ c\ и\]
\[\ d > 0,\ то\ ac < bd.\]
\[Доказательство:\]
\[Умножаем\ обе\ части\ \]
\[неравенства\ a < b\ на\ число\ \]
\[c \Longrightarrow ac < bc;\]
\[умножаем\ обе\ части\ \]
\[нерванества\ c < d\ на\ число\ \]
\[b \Longrightarrow bc < bd.\]
\[Получаем:ac < bc < bd \Longrightarrow\]
\[\Longrightarrow ac < bd - ч.т.д.\]
\[\boxed{\text{3.\ }}\]
\[4 < a < 5;\ \ \ \ \ \ 9 < b < 10\]
\[1) + \left| \begin{matrix} 4 < a < 5 \\ 9 < b < 10 \\ \end{matrix} \right.\ \]
\(\overline{13 < a + b < 15}\)
\[2) + \left| \begin{matrix} \ \ \ \ 4 < a < 5\ \\ - 10 < - b < - 9 \\ \end{matrix} \right.\ \]
\[\text{\ \ \ \ \ }\overline{\ - 6 < a - b < - 4}\]
\[3)*\left| \begin{matrix} 4 < a < 5 \\ 9 < b < 10 \\ \end{matrix} \right.\ \]
\[\text{\ \ \ \ \ \ }\overline{\ \ \ 36 < ab < 50}\]
\[4)\frac{a}{b} = a \cdot \frac{1}{b}\]
\[*\left\{ \begin{matrix} \frac{1}{10} < \frac{1}{b} < \frac{1}{9} \\ 4 < a < 5 \\ \end{matrix} \right.\ \]
\[\text{\ \ \ \ }\overline{\frac{4}{10} < \frac{a}{b} < \frac{5}{9}}\]
\[\boxed{\text{4.\ }}\]
\[Абсолютная\ погрешность\ \]
\[приближенного\ значения -\]
\[так\ называют\ модуль\ \]
\[разности\ точного\ \]
\[и\ приближенного\ значений.\]
\[x = a \pm h,\ \ это\ точное\ \]
\[значение\ переменной\ x,\ \]
\[в\ диапазоне\ от\]
\[\ a - h\ \ до\ a + h,\ \ то\ есть:\]
\[a - h \leq x \leq a + h.\]
\[\boxed{\text{5.\ }}\]
\[Относительная\ погрешность\ \]
\[приближенного\ значения -\]
\[так\ называется\ отношение\ \]
\[абсолютной\ погрешности\ \]
\[к\ модулю\ приближенного\ \]
\[значения.\]
