Решебник по алгебре 7 класс Мерзляк ФГОС Задание 92

 

\[\boxed{\text{92\ (}\text{н}\text{).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ \text{x\ }рублей\ цена\ одного\ \]

\[вида\ конфет,\ тогда\ (x - 144)\ \]

\[рублей - цена\ второго\ вида\ \]

\[конфет.\ \ За\ конфеты\ первого\ \]

\[вида\ заплатили\ 2\text{x\ }рублей,\ а\ за\ \]

\[конфеты\ второго\ вида\ \]

\[заплатили\ 3,5 \cdot (x - 144)\ \]

\[рублей.\]

\[Известно,\ что\ заплатили\ \]

\[одинаково.\]

\[Составим\ уравнение:\]

\(2x = 3,5 \cdot (x - 144)\)

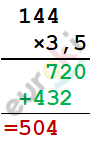
\[2x = 3,5x - 504\]

\[3,5x - 2x = 504\]

\[1,5x = 504\]

\[x = 504\ :1,5\]

\[x = 504\ :1,5 = 5040\ :15 =\]

\[= 336\ (рублей) - стоит\ \]

\[килограмм\ конфет\ первого\ \]

\[вида.\]

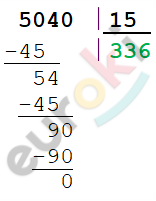
\[336 - 144 = 192\ (рубля) -\]

\[стоит\ килограмм\ конфет\ \]

\[второго\ вида.\]

\[Ответ:\ \ 336\ рублей\ и\ 192\ \]

\[рубля.\]

\[\boxed{\text{92\ (}\text{с}\text{).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ \text{x\ }рублей\ цена\ второго\ \]

\[вида\ конфет,\ тогда\ (x + 48)\ \]

\[рублей - цена\ первого\ вида\ \]

\[конфет.\ 2\ кг\ конфет\ первого\ \]

\[вида\ стоят\ столько\ же,\ \]

\[сколько\ 3,5\ кг\ второго\ вида.\]

\[Составим\ уравнение:\]

\[2 \cdot (x + 48) = 3,5x\]

\[2x + 96 = 3,5x\]

\[3,5x - 2x = 96\]

\[1,5x = 96\]

\[x = 96\ :1,5 = 960\ :15 =\]

\[= 64\ (рубля) - \ цена\ второго\ \]

\[вида\ конфет.\]

\[64 + 48 = 112\ (рублей) - цена\ \]

\[первого\ вида\ конфет.\]

\[Ответ:112\ рублей;\ 64\ рубля.\]

\[\boxed{\text{92.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Краткая запись.

\[Капуста - 64\ кг\]

\[Морковь - ?кг;\ \frac{5}{8}\ от\ 64\ кг\]

\[Картофель - ?кг;\ \ 180\% =\]

\[= 1,8\ \ от\ моркови\]

Решение.

\[1)\ 64 \cdot \frac{5}{8} = \frac{64 \cdot 5}{8} = 8 \cdot 5 =\]

\[= 40\ (кг) - \ масса\ моркови.\]

\[2)\ 40 \cdot 1,8 = 4 \cdot 18 =\]

\[= 72\ (кг) - масса\ картофеля.\]

\[3)\ 64 + 40 + 72 = 176\ (кг) -\]

\[всего\ овощей\ завезли\ в\ \]

\[столовую.\]

\[Ответ:176\ кг.\]