Решебник по алгебре 7 класс Мерзляк ФГОС Задание 379

 

\[\boxed{\text{379\ (379).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ x\ см - длина\ \]

\[прямоугольника\ ,\ тогда\ \]

\[(x - 8)\ см - его\ ширина.\]

\[x(x - 8)\ см^{2} - исходная\ \]

\[площадь\ прямоугольника;\]

\[x + 6\ (см) - длина\ \]

\[прямоугольника\ после\ \]

\[увеличения;\]

\[x(x + 6)\ см^{2} - площадь\ \]

\[прямоугольника\ после\ \]

\[увеличения.\]

\[Площадь\ прямоугольника\ \]

\[увеличится\ на\ 72\ см^{2}.\]

\[Составим\ уравнение:\]

\[x \cdot (x - 8) + 72 =\]

\[= (x + 6) \cdot (x - 8)\]

\[- 6x = - 120\]

\[x = 20\ (см) - исходная\ длина\ \]

\[прямоугольника.\]

\[20 - 8 = 12\ (см) - исходная\ \]

\[ширина.\]

\[(20 + 12) \cdot 2 = 32 \cdot 2 =\]

\[= 64\ (см) - периметр\ \]

\[исходного\ прямоугольника.\]

\[Ответ:64\ см.\ \]

\[\boxed{\text{379.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Всего\ на\ доске\ 64\ клетки\ \]

\[(8 \cdot 8).\]

\[Белую\ ладью\ можно\ поставить\]

\[\ на\ любую\ клетку:64\ способа.\]

\[Она\ будет\ бить\ 7\ клеток\ по\ \]

\[вертикали,\ 7\ клеток\ по\ \]

\[горизонтали,\ тогда:\]

\[64 - 7 - 7 - 1 = 49\ клеток.\]

\[То\ есть,\ черную\ ладью\ можно\ \]

\[поставить\ 49\ способами,\ \]

\[общее\ количество\ способов:\]

\(49 \cdot 64 = 3136\).

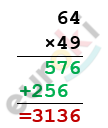
\[Ответ:3136\ способов.\ \]