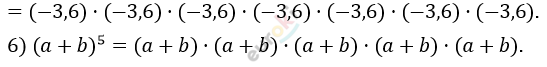Решебник по алгебре 7 класс Мерзляк ФГОС Задание 230

 

\[\boxed{\text{230\ (230).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ \text{x\ }ребро\ куба,\ тогда\ его\ \]

\[объем\ был:\]

\[V_{к} = x \cdot x \cdot x = x^{3}.\]

\[mx - увеличенное\ ребро,\ а\ \]

\[объем\ стал\ равен:\]

\[V_{к} = \left( \text{mx} \right)^{3} = m^{3} \cdot x^{3};\ то\ есть\ \]

\[\ увеличился\ в\ m^{3}\ раз.\]

\[Ответ:в\ m^{3}\ раз.\]

\[\boxed{\text{230.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[Представим\ каждую\ степень\ в\ виде\ произведения,\ множитель\]

\[которого\ равен\ основанию\ степени,\ а\ количество\ таких\ множителей\]

\[равно\ показателю\ степени.\]

\[1)\ 11^{6} =\]

\[= 11 \cdot 11 \cdot 11 \cdot 11 \cdot 11 \cdot 11.\]

\[2)\ (0,1)^{4} = 0,1 \cdot 0,1 \cdot 0,1 \cdot 0,1.\]

\[3)\ \left( - \frac{1}{6} \right)^{2} = \left( - \frac{1}{6} \right) \cdot \left( - \frac{1}{6} \right).\]

\[4)\ (5c)^{3} = 5c \cdot 5c \cdot 5c.\]

\[5)\ ( - 3,6)^{7} =\]