Решебник по алгебре 7 класс Мерзляк ФГОС Задание 164

 

\[\boxed{\text{164\ (164).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[x^{2} - x^{3} = {0,1}^{2} - {0,1}^{3} =\]

\[= 0,01 - 0,001 = 0,009.\]

\[15a^{2} = 15 \cdot {0,4}^{2} = 15 \cdot 0,16 =\]

\[= 2,4.\]

\[(x - y)^{5} = (0,8 - 0,6)^{5} =\]

\[= {0,2}^{5} = 0,00032.\]

\[a^{2}b^{3} = {0,6}^{2} \cdot {0,5}^{3} =\]

\[= 0,36 \cdot 0,125 = 0,045\text{.\ }\]

\[\left( x^{2} - y^{2} \right)\ :(x - y) =\]

\[= \frac{(x - y) \cdot (x + y)}{x - y} = x + y =\]

\[= 5 + 3 = 8.\]

\[\left( x^{2} - y^{2} \right)\ :x - y =\]

\[= \left( 5^{2} - 3^{3} \right)\ :5 - 3 =\]

\[= (25 - 9)\ :5 - 3 =\]

\[= 16\ :5 - 3 = 3,2 - 3 = 0,2.\]

\[x^{2} - y^{2}\ :(x - y) =\]

\[= 25 - 9\ :(5 - 3) =\]

\[= 25 - 9\ :2 = 25 - 4,5 =\]

\[= 20,5.\]

\[x^{2} - y^{2}\ :x - y =\]

\[= 25 - 9\ :5 - 3 =\]

\[= 25 - 1,8 - 3 = 20,2.\]

\[\boxed{\text{164.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ \text{x\ }мест\ в\ ряду\ во\ втором\ \]

\[зале,\ тогда\ (x + 4)\ мест\ в\ ряду\ \]

\[в\ первом\ зале.\]

\[В\ первом\ зале\ 12\ рядов,\ а\ во\ \]

\[втором\ 15\ рядов.\ \]

\[Всего\ 534\ места.\]

\[Составим\ уравнение:\]

\[15x + 12 \cdot (x + 4) = 534\]

\[15x + 12x + 48 = 534\]

\[27x = 534 - 48\]

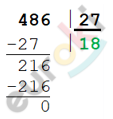
\[27x = 486\]

\[x = 486\ :27 = 18\ (мест) - \ в\ \]

\[одном\ ряду\ во\ втором\ зале.\]

\[18 \cdot 15 = 270\ (мест) - \ во\ \]

\[втором\ зале\ всего.\]

\[18 + 4 = 22\ (места) - в\ одном\ \]

\[ряду\ в\ первом\ зале.\]

\[22 \cdot 12 = 264\ (места) - \ в\ \]

\[первом\ зале\ всего.\]

\(Ответ:264\ места;\ 270\ мест.\)