Решебник по алгебре 7 класс Мерзляк ФГОС Задание 113

 

\[\boxed{\text{113\ (113).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Пусть\ x\ кг\ груш\ было\ в\ первой\ \]

\[корзине,\ тогда\ (24 - x)\ кг\ \]

\[груш\ было\ во\ второй\ корзине.\ \]

\[Значит,\ \left( \frac{3}{7}x \right)\ кг\ груш\ \]

\[переложили\ во\ вторую\ \]

\[корзину\ и\ масса\ во\ второй\ \]

\[корзине\ стала\ в\ 2\ раза\ больше,\ \]

\[чем\ в\ первой.\]

\[Составим\ уравнение:\]

\[2 \cdot \left( x - \frac{3}{7}x \right) = (24 - x) + \frac{3}{7}x\]

\[2x - \frac{6}{7}x = 24 - x + \frac{3}{7}x\ \ \ \ \ \ \ | \cdot 7\]

\[14x - 6x = 168 - 7x + 3x\]

\[8x + 7x - 3x = 168\]

\[12x = 168\]

\[x = 14\ (кг) - груш\ было\ в\ \]

\[первой\ корзине.\]

\[24 - 14 = 10\ (кг) - груш\ было\ \]

\[во\ второй\ корзине.\]

\[Ответ:14\ кг;10\ кг.\ \]

\[\boxed{\text{113.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[1)\ 0,9x - 0,6 \cdot (x - 3) =\]

\[= 2 \cdot (0,2x - 1,3)\]

\[0,9x - 0,6x + 1,8 = 0,4x - 2,6\]

\[0,3x - 0,4x = - 2,6 - 1,8\]

\[- 0,1x = - 4,4\]

\[x = \frac{4,4}{0,1}\]

\[x = 44\]

\[Ответ:x = 44.\]

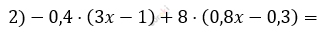
\[= 5 - (3,8x + 4)\]

\[- 1,2x + 0,4 + 6,4x - 2,4 =\]

\[= 5 - 3,8x - 4\]

\[5,2x + 3,8x = 1 + 2\]

\[9x = 3\]

\[x = \frac{3}{9} = \frac{1}{3}\]

\[Ответ:x = \frac{1}{3}.\]

\[3)\ \frac{4}{7} \cdot (0,56 - 4,2y) + 0,4 =\]

\[= \frac{5}{13} \cdot (0,52 - 6,5y)\]

\[\frac{4}{7} \cdot \left( \frac{56}{100} - \frac{42}{10}y \right) + \frac{4}{10} =\]

\[= \frac{5}{13} \cdot \left( \frac{52}{100} - \frac{65}{10}y \right)\]

\[\frac{4 \cdot 56}{7 \cdot 100} - \frac{4 \cdot 42}{7 \cdot 10}y + \frac{4}{10} =\]

\[= \frac{5 \cdot 52}{13 \cdot 100} - \frac{5 \cdot 65}{13 \cdot 10}y\]

\[\frac{8}{25} - \frac{12}{5}y + \frac{4}{10} = \frac{1}{5} - \frac{5}{2}y\]

\[0,32 - 2,4y + 0,4 = 0,2 - 2,5y\]

\[- 2,4y + 2,5y = 0,2 - 0,32 - 0,4\]

\[0,1y = - 0,52\]

\[y = - \frac{0,52}{0,1}\]

\[y = - 5,2\]

\[Ответ:\ y = - 5,2.\]