Решебник по алгебре 7 класс Макарычев ФГОС Задание 984

 

\[\boxed{\text{984.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

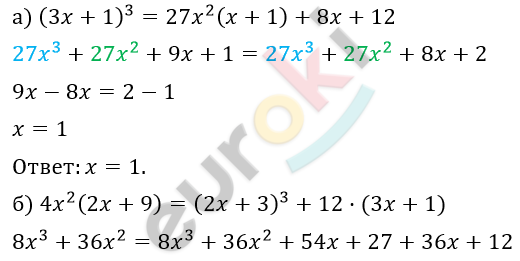
\[54x + 36x = - 27 - 12\]

\[90x = - 39\ \]

\[x = - \frac{13}{30}\]

\[Ответ:x = - \frac{13}{30}.\]

\[\boxed{\text{984\ (984).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

При решении используем следующее:

1. Формулу квадрата суммы:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

\[\mathbf{(}\mathbf{a}\mathbf{+}\mathbf{b}\mathbf{)}^{\mathbf{2}}\mathbf{=}\mathbf{a}^{\mathbf{2}}\mathbf{+}\mathbf{2}\mathbf{\text{ab}}\mathbf{+}\mathbf{b}^{\mathbf{2}}\mathbf{.}\]

2. Формулу квадрата разности:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

\[\mathbf{(}\mathbf{a}\mathbf{-}\mathbf{b}\mathbf{)}^{\mathbf{2}}\mathbf{=}\mathbf{a}^{\mathbf{2}}\mathbf{-}\mathbf{2}\mathbf{\text{ab}}\mathbf{+}\mathbf{b}^{\mathbf{2}}\mathbf{.}\]

3. Чтобы привести (сложить или вычесть) подобные слагаемые (числа, которые имеют одинаковую буквенную часть (x, y, a и т. д.)), надо вычесть или сложить их коэффициенты (числа перед буквами) и полученный результат умножить на общую буквенную часть.

4. Признак делимости произведения – если хотя бы один из множителей делится на некоторое число без остатка, то и произведение делится на это число.

Решение.

\[\textbf{а)}\ (n + 1)^{2} - (n - 1)^{2} =\]

\[= n^{2} + 2n + 1 - n^{2} + 2n - 1 =\]

\[= 4n \Longrightarrow делится\ на\ 4.\]

\[\textbf{б)}\ (2n + 3)^{2} - (2n - 1)^{2} =\]

\[= 4n^{2} + 12n + 9 - 4n^{2} + 4n - 1 =\]

\[= 16n + 9 =\]

\[= 8 \cdot (2n + 1) \Longrightarrow делится\ на\ 8.\]

\[\textbf{в)}\ (3n + 1)^{2} - (3n - 1)^{2} =\]

\[= 9n^{2} + 6n + 1 - 9n^{2} + 6n - 1 =\]

\[= 12n \Longrightarrow делится\ на\ 12.\]

\[\textbf{г)}\ (5n + 1)^{2} - (2n - 1)^{2} =\]

\[= 7n(3n + 2) \Longrightarrow делится\ на\ 7.\]