Решебник по алгебре 7 класс Макарычев ФГОС Задание 812

 

\[\boxed{\text{812.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Решение.

\[\left( x^{3} + 4x^{2} - 17x + 41 \right)(x + a) =\]

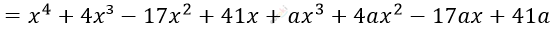
\[Чтобы\ этот\ многочлен\ был\ \]

\[равен\ многочлену,\ не\ \]

\[содержащему\ x^{3},нужно:\]

\[4x^{3} + ax^{3} = 0\]

\[x^{3}(4 + a) = 0\]

\[x = 0\ \ \ или\ \ \ a = - 4\]

\[Ответ:при\ a = - 4.\]

\(\boxed{\text{812\ (812).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\)

Пояснение.

Многочлен – это выражение, которое является суммой нескольких одночленов (выражение, состоящие из произведения числа на одну или несколько переменных (буквы a, b, c, и тд)).

Преобразуем в многочлен с помощью:

1. Формулы квадрата суммы:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

\[\mathbf{(}\mathbf{a}\mathbf{+}\mathbf{b}\mathbf{)}^{\mathbf{2}}\mathbf{=}\mathbf{a}^{\mathbf{2}}\mathbf{+}\mathbf{2}\mathbf{\text{ab}}\mathbf{+}\mathbf{b}^{\mathbf{2}}\]

2. Формулы квадрата разности:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

\[\mathbf{(}\mathbf{a}\mathbf{-}\mathbf{b}\mathbf{)}^{\mathbf{2}}\mathbf{=}\mathbf{a}^{\mathbf{2}}\mathbf{-}\mathbf{2}\mathbf{\text{ab}}\mathbf{+}\mathbf{b}^{\mathbf{2}}\]

При возведении степени в степень (степень говорит нам о том, сколько раз следует умножить число само на себя: \(a^{3} = a \bullet a \bullet a\)) показатели перемножаются, а основание остается прежним:

\[\mathbf{(}\mathbf{a}^{\mathbf{m}}\mathbf{)}^{\mathbf{n}}\mathbf{=}\mathbf{a}^{\mathbf{m \bullet n}}\mathbf{.}\]

Решение.

\[\textbf{а)}\ \left( a^{2} - 3a \right)^{2} =\]

\[= \left( a^{2} \right)^{2} - 6a^{2}a + (3a)^{2} =\]

\[= a^{4} - 6a^{3} + 9a²\]

\[\textbf{б)}\ \left( \frac{1}{2}x^{3} + 6x \right)^{2} =\]

\[= \left( \frac{1}{2}x^{3} \right)^{2} + 2 \cdot \frac{1}{2} \cdot 6x^{3} \cdot x + (6x)^{2} =\]

\[= \frac{1}{4}x^{6} + 6x^{4} + 36x²\]

\[\textbf{в)}\ \left( c^{2} - 0,7c^{3} \right)^{2} =\]

\[= \left( c^{2} \right)^{2} - 2 \cdot 0,7c^{2}c^{3} + \left( 0,7c^{3} \right)^{2} =\]

\[= c^{4} - 1,4c^{5} + 0,49c^{6}\]

\[\textbf{г)}\ \left( 4y^{3} - 0,5y^{2} \right)^{2} =\]

\[= 16y^{6} - 4y^{5} + 0,25y^{4}\]

\[\textbf{д)}\ \left( 1\frac{1}{2}a^{5} + 8a^{2} \right)^{2} =\]

\[= \left( \frac{3}{2}a^{5} + 8a^{2} \right)^{2} =\]

\[= \frac{9}{4}a^{10} + 24a^{7} + 64a^{4}\]

\[\textbf{е)}\ \left( 0,6b - 60b^{2} \right)^{2} =\]

\[= 0,36b^{2} - 72b^{3} + 3600b^{4}\]