Решебник по алгебре 7 класс Макарычев ФГОС Задание 810

 

\[\boxed{\text{810.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

Решение.

\[\textbf{а)}\ a(x + 6) + x(x - 3a) = 9\ \]

\[при\ x = 2a - 3:\]

\[a(2a + 3) + (2a - 3)( - 3 - a) =\]

\[= 9\]

\[9 = 9\]

\[Верно.\]

\[\textbf{б)}\ x(x - 3a) + a(a + x) + 4 =\]

\[= 13\ \ \]

\[при\ \ x = a + 3:\]

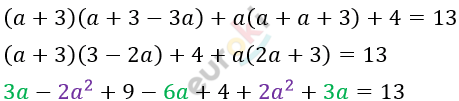
\[13 = 13\]

\[Верно.\]

\[\boxed{\text{810\ (810).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

При вычислении используем:

1. Формулу квадрата суммы:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

\[\mathbf{(}\mathbf{a}\mathbf{+}\mathbf{b}\mathbf{)}^{\mathbf{2}}\mathbf{=}\mathbf{a}^{\mathbf{2}}\mathbf{+}\mathbf{2}\mathbf{\text{ab}}\mathbf{+}\mathbf{b}^{\mathbf{2}}\]

2. Формулу квадрата разности:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

\[\mathbf{(}\mathbf{a}\mathbf{-}\mathbf{b}\mathbf{)}^{\mathbf{2}}\mathbf{=}\mathbf{a}^{\mathbf{2}}\mathbf{-}\mathbf{2}\mathbf{\text{ab}}\mathbf{+}\mathbf{b}^{\mathbf{2}}\]

Решение.

\[\textbf{а)}\ (100 + 1)^{2} =\]

\[= 10\ 000 + 200 + 1 = 10\ 201\]

\[\textbf{б)}\ (100 - 1)^{2} =\]

\[= 10\ 000 - 200 + 1 = 9801\]

\[\textbf{в)}\ 61² = (60 + 1)^{2} =\]

\[= 3600 + 120 + 1 = 3721\]

\[\textbf{г)}\ 199² = (200 - 1)^{2} =\]

\[= 40\ 000 - 400 + 1 = 39\ 601\]

\[\textbf{д)}\ 999^{2} = (1000 - 1)^{2} =\]

\[= 1\ 000\ 000 - 2000 + 1 =\]

\[= 998\ 001\]

\[\textbf{е)}\ 702² = (700 + 2)^{2} =\]

\[= 490\ 000 + 2800 + 4 =\]

\[= 492\ 804\]

\[\textbf{ж)}\ 9,9² = (10 - 0,1)^{2} =\]

\[= 100 - 2 + 0,01 = 98,01\]

\[\textbf{з)}\ 10,2² = (10 + 0,2)^{2} =\]

\[= 100 + 4 + 0,04 = 104,04\]