Решебник по алгебре 7 класс Макарычев ФГОС Задание 785

 

\[\boxed{\text{785.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

Правило вынесения общего множителя за скобки:

• найдем НОД числовых коэффициентов;

• проанализируем буквенные части одночленов (если выражение представляет собой многочлен);

• поделим каждый одночлен на НОД и общие буквы в наименьших степенях;

• вынесем общий множитель за скобки, внутрь скобок поместим результаты деления и исходный знак (если была сумма — то плюс, если разность — минус).

Используем распределительный закон:

\[ab + ac = a(b + c);\]

\[ab - ac = a(b - c).\]

Решение.

\[\textbf{а)}\ (a - 3b)(a + 2b) + 5a(a + 2b) =\]

\[= (a + 2b)(a - 3b + 5a) =\]

\[= (a + 2b)(6a - 3b) =\]

\[= 3 \cdot (a + 2b)(2a - b)\]

\[\textbf{б)}\ (x + 8y)(2x - 5b) - 8y(2x - 5b) =\]

\[= (2x - 5b)(x + 8y - 8y) =\]

\[= x \cdot (2x - 5b)\]

\[\textbf{в)}\ 7a^{2}(a - x) + \left( 6a^{2} - ax \right)(x - a) =\]

\[= 7x^{2}(a - x) + \left( ax - 6a^{2} \right)(a - x) =\]

\[= (a - x)\left( 7a^{2} + ax - 6a^{2} \right) =\]

\[= (a - x)\left( a^{2} + ax \right) =\]

\[= a \cdot (a - x)(a + x)\]

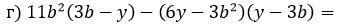
\[= (3b - y)\left( 11b^{2} + 6y - 3b^{2} \right) =\]

\[= (3b - y)\left( 8b^{2} + 6y \right) =\]

\[= 2 \cdot (3b - y)(4b^{2} + 3y)\]

\[\boxed{\text{785\ (785).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ Пусть\ n,\ n + 1,\ n + 2,\ \]

\[n + 3 - четыре\ \]

\[последовательных\ целых\ \]

\[числа.\]

\[(n + 1)(n + 2) - n(n + 3) =\]

\[Что\ и\ требовалось\ доказать.\]

\[\textbf{б)}\ Пусть\ 2n - 1,\ 2n + 1,\ 2n + 3 -\]

\[три\ последовательных\ \]

\[нечетных\ числа.\]

\[(2n + 1)^{2} - (2n - 1)(2n + 3) =\]

\[Что\ и\ требовалось\ доказать.\]