Решебник по алгебре 7 класс Макарычев ФГОС Задание 711

 

\[\boxed{\text{711.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

Решение.

\[\textbf{а)}\ n(n - 1) - (n + 3)(n + 2) =\]

\[= n^{2} - n - \left( n^{2} + 2n + 3n + 6 \right) =\]

\[= n^{2} - n - n^{2} - 5n - 6 =\]

\[= - 6n - 6 =\]

\[= - 6 \cdot (n + 1) \Longrightarrow делится\ на\ 6\]

\[при\ любом\ значении\ n.\]

\[\textbf{б)}\ n(n + 2) - (n - 7)(n - 5) =\]

\[= n^{2} + 2n - \left( n^{2} - 5n - 7n + 35 \right) =\]

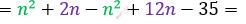
\[= 14n - 35 = 7 \cdot (2n - 5) \Longrightarrow\]

\[делится\ на\ 7\ при\ любом\ \]

\[значении\ n.\]

\[Что\ и\ требовалось\ доказать.\]

\[\boxed{\text{711\ (711).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[\textbf{а)}\ x^{3} + x^{2} + x + 1 =\]

\[= \left( x^{3} + x^{2} \right) + 1 \cdot (x + 1) =\]

\[= x^{2}(x + 1) + x + 1 =\]

\[= (x^{2} + 1)(x + 1)\]

\[\textbf{б)}\ y^{5} - y^{3} - y^{2} + 1 =\]

\[= \left( y^{5} - y^{3} \right) - \left( y^{2} - 1 \right) =\]

\[= y^{3}\left( y^{2} - 1 \right) - {(y}^{2} - 1) =\]

\[= (y^{2} - 1)(y^{3} - 1)\]

\[\textbf{в)}\ a^{4} + 2a^{3} - a - 2 =\]

\[= \left( a^{4} - a \right) + \left( 2a^{3} - 2 \right) =\]

\[= a\left( a^{3} - 1 \right) + 2 \cdot \left( a^{3} - 1 \right) =\]

\[= (a^{3} - 1)(a + 2)\]

\[\textbf{г)}\ b^{6} - 3b^{4} - 2b^{2} + 6 =\]

\[= \left( b^{6} - 2b^{4} \right) - \left( 3b^{4} - 6 \right) =\]

\[= b^{2}\left( b^{4} - 2 \right) - 3 \cdot \left( b^{4} - 2 \right) =\]

\[= (b^{4} - 2)(b^{2} - 3)\]

\[\textbf{д)}\ a^{2} - ab - 8a + 8b =\]

\[= \left( a^{2} - 8a \right) - (ab - 8b) =\]

\[= a(a - 8) - b(a - 8) =\]

\[= (a - 8)(a - b)\]

\[\textbf{е)}\ ab - 3b + b^{2} - 3a =\]

\[= (ab - 3a) + \left( b^{2} - 3b \right) =\]

\[= a(b - 3) + b(b - 3) =\]

\[= (b - 3)(a + b)\]

\[\textbf{ж)}\ 11x - xy + 11y - x^{2} =\]

\[= (11x + 11y) - \left( x^{2} + xy \right) =\]

\[= 11 \cdot (x + y) - x(x + y) =\]

\[= (x + y)(11 - x)\]

\[\textbf{з)}\ kn - mn - n^{2} + mk =\]

\[= \left( kn - n^{2} \right) + (mk - mn) =\]

\[= n(k - n) + m(k - n) =\]

\[= (k - n)(n + m)\ \]