Решебник по алгебре 7 класс Макарычев ФГОС Задание 636

 

\[\boxed{\text{636.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Для того, чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным:

\[a^{n} \cdot b^{n} = (a \cdot b)^{n}.\]

При умножении чисел с разными знаками получается отрицательное число.

При умножении чисел с одинаковыми знаками получается положительное число.

Решение.

\[\textbf{а)}\ 14y + 2y(6 - y) =\]

\[= 14y + 2y \cdot 6 - 2y \cdot y =\]

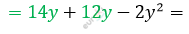
\[= - 2y^{2} + 26y\]

\[\textbf{б)}\ 3y² - 2y(5 + 2y) =\]

\[= 3y^{2} - 2y \cdot 5 - 2y \cdot 2y =\]

\[= - y^{2} - 10y\]

\[\textbf{в)}\ 4x(x - 1) - 2 \cdot \left( 2x^{2} - 1 \right) =\]

\[= 4x \cdot x - 4x - 2 \cdot 2x^{2} + 2 =\]

\[\textbf{г)}\ 5a\left( a^{2} - 3a \right) - 3a\left( a^{2} - 5a \right) =\]

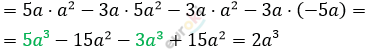
\[\textbf{д)}\ 7b(4c - b) + 4c(c - 7b) =\]

\[\textbf{е)} - 2y\left( x^{3} - 2y \right) - \left( x^{3}y + 4y^{2} \right) =\]

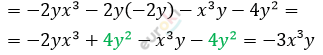
\[\textbf{ж)}\ 3m^{2}(m + 5n) - 2n\left( 8m^{2} - n \right) =\]

\[= 3m^{3} - m^{2}n + 2n²\]

\[\textbf{з)}\ 6m²n³ - n^{2}\left( 6m^{2}n + n - 1 \right) =\]

\[\boxed{\text{636\ (636).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ \frac{3x + 5}{5} - \frac{x + 1}{3} = 1\ \ \ \ \ | \cdot 15\]

\[3 \cdot (3x + 5) - 5 \cdot (x + 1) = 15\]

\[9x + 15 - 5x - 5 = 15\]

\[4x = 15 - 10\]

\[4x = 5\]

\[x = \frac{5}{4}\]

\[x = 1,25\]

\[Ответ:x = 1,25.\]

\[\textbf{б)}\ \frac{2p - 1}{6} - \frac{p + 1}{3} = p\ \ \ \ \ | \cdot 6\]

\[2p - 1 - 2 \cdot (p + 1) = 6p\]

\[2p - 1 - 2p - 2 - 6p = 0\]

\[- 6p = 3\]

\[p = 3\ :( - 6) = - \frac{3}{6} = - \frac{1}{2}\]

\[p = - 0,5\]

\[Ответ:p = - 0,5.\]

\[\textbf{в)}\ \frac{6y - 1}{15} - \frac{y}{5} = \frac{2y}{3}\ \ \ \ \ | \cdot 15\]

\[6y - 1 - 3y = 5 \cdot 2y\]

\[3y - 1 - 10y = 0\]

\[- 7y = 1\]

\[y = - \frac{1}{7}\]

\[Ответ:y = - \frac{1}{7}.\]

\[\textbf{г)}\ \frac{12 - x}{4} - \frac{2 - x}{3} = \frac{x}{6}\ \ \ \ \ \ | \cdot 12\]

\[3 \cdot (12 - x) - 4 \cdot (2 - x) = 2x\]

\[36 - 3x - 8 + 4x - 2x = 0\ \]

\[- x = - 28\]

\[x = 28\]

\[Ответ:x = 28.\]