Решебник по алгебре 7 класс Макарычев ФГОС Задание 617

 

\[\boxed{\text{617.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

Неизвестное значение M оставим слева, все остальные одночлены перенесем вправо, меняя знак на противоположный. Выполним приведение подобных слагаемых.

Подобными членами называются слагаемые многочлена, которые имеют одинаковую буквенную часть.

Если перед скобками стоит знак «+», то скобки можно убрать, сохранив знаки слагаемых в них.

Если перед скобками стоит знак «-», то скобки можно убрать, при этом изменив знаки слагаемых на противоположные.

Решение.

\[Обозначим\ искомый\ \]

\[многочлен\ через\ M.\]

\[\textbf{а)}\ \left( x^{2} + y^{2} - 2xy + 1 \right) + M =\]

\[= y^{2} + 1\]

\[M = - x^{2} + 2xy\]

\[\textbf{б)}\ \left( x^{2} + y^{2} - 2xy + 1 \right) + M =\]

\[= x² + 1\]

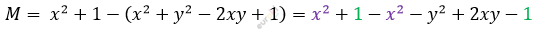
\[M = - y^{2} + 2xy\]

\[\boxed{\text{617\ (617).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[\textbf{а)} - 3x^{2}\left( - x^{3} + x - 5 \right) =\]

\(= 3x^{5} - 3x^{3} + 15x^{2}\)

\[\textbf{б)}\ \left( 1 + 2a - a^{2} \right) \cdot 5a =\]

\[= 5a + 2a \cdot 5a - a^{2} \cdot 5a =\]

\[= 5a + 10a^{2} - 5a^{3}\]

\[\textbf{в)}\ \frac{2}{3}x^{2}y \cdot (15x - 0,9y + 6) =\]

\[= 10x^{3}y - 0,6x^{2}y^{2} + 4x^{2}y\]

\[\textbf{г)}\ 3a^{4}x \cdot \left( a^{2} - 2ax + x^{3} - 1 \right) =\]

\[= 3a^{6}x - 6a^{5}x^{2} + 3a^{4}x^{4} - 3a^{4}x\]

\[\textbf{д)}\ \left( x^{2}y - xy + xy^{2} + y^{3} \right) \cdot 3xy^{2} =\]

\[= 3x^{3}y^{3} - 3x^{2}y^{3} + 3x^{2}y^{4} + 3xy^{5}\]

\[\textbf{е)} - \frac{3}{7}a^{4} \cdot \left( 2,1b^{2} - 0,7a + 35 \right) =\]

\[= - 0,9a^{4}b^{2} + 0,3a^{5} - 15a^{4}\]