Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 7 класс Макарычев ФГОС Задание 582
Задание 582
\[\boxed{\text{582.}\text{\ }еуроки - ответы\ на\ пятёрку}\]
Пояснение.
План решения уравнения графическим способом:
записать каждую часть уравнения в виде графической функции (y=kx);
построить графики функций в одной системе координат;
найти точки их пересечения;
записать в ответе значение точки x.
Решение.
\[\textbf{а)}\ x^{2} = 2 - x\]
\[y = x^{2}\]
| \[x\] | \[- 2\] | \[- 1\] | \[0\] | \[1\] | \[2\] |
|---|---|---|---|---|---|
| \[y\] | \[4\] | \[1\] | \[0\] | \[1\] | \[4\] |
\[y = 2 - x\]
| \[x\] | \[0\] | \[2\] |
|---|---|---|
| \[y\] | \[2\] | \[0\] |
\[Корень:\ \ \ - 2;1.\]
\[\textbf{б)}\ x² = 8\]
\[y = x^{2}\]
| \[x\] | \[- 2\] | \[- 1\] | \[0\] | \[1\] | \[2\] |
|---|---|---|---|---|---|
| \[y\] | \[4\] | \[1\] | \[0\] | \[1\] | \[4\] |
\[y = 8\]
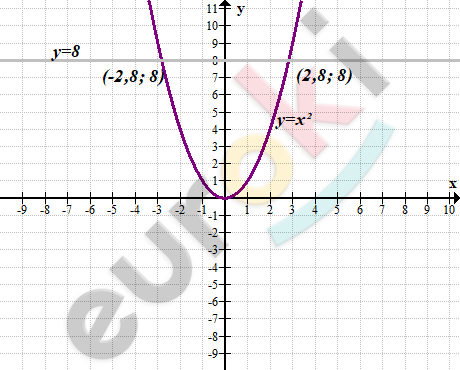
\[Корень:\ \ \pm 2;8.\]
\[\textbf{в)}\ x³ = 6\]
\[y = x^{3}\]
| \[x\] | \[- 2\] | \[- 1\] | \[0\] | \[1\] | \[2\] |
|---|---|---|---|---|---|
| \[y\] | \[- 8\] | \[- 1\] | \[0\] | \[1\] | \[8\] |
\[y = 6\ \]
\[Корень:\ \ 1,8.\]
\[\textbf{г)}\ x³ = - x + 4\]
\[y = x^{3}\]
| \[x\] | \[- 2\] | \[- 1\] | \[0\] | \[1\] | \[2\] |
|---|---|---|---|---|---|
| \[y\] | \[- 8\] | \[- 1\] | \[0\] | \[1\] | \[8\] |
\[y = - x + 4\]
| \[x\] | \[0\] | \[4\] |
|---|---|---|
| \[y\] | \[4\] | \[0\] |
\[Корень:\ 1,4.\]
\[\boxed{\text{582\ (582).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[\textbf{а)}\ 0,3y = 70\]
\[y = \frac{70}{0,3} = \frac{700}{3}\]
\[y = 233\frac{1}{3}\]
\[Ответ:y = 233\frac{1}{3}.\]
\[\textbf{б)}\ \frac{5}{8}x = - 1\]
\[x = - 1\ :\frac{5}{8} = - \frac{8}{5}\]
\[x = \ - 1\frac{3}{5}\]
\[Ответ:x = - 1,6.\]
\[\textbf{в)}\ \frac{1}{9}a = - \frac{3}{7}\]
\[a = - \frac{3}{7}\ :\frac{1}{9} = - \frac{3}{7} \cdot 9 = - \frac{27}{7}\]
\[a = - 3\frac{6}{7}\]
\[Ответ:a = - 3\frac{6}{7}.\]
