Решебник по алгебре 7 класс Макарычев ФГОС Задание 407

 

\[\boxed{\text{407.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

Пояснение.

Площадь круга вычисляется по формуле:

\[S = \pi r^{2};\ \ \pi \approx 3,14;\ \ r - радиус\ круга.\]

Чтобы найти площадь прямоугольника, нужно длину умножить на ширину:

\[S = a \cdot b.\]

Решение.

\[a - ширина\ окна;\]

\[1,5a - высота\ окна;\]

\[\frac{a}{2} - радиус\ полукруга;\]

\[a \cdot 1,5a - площадь\ \]

\[прямоугольной\ части\ окна;\]

\[\frac{\pi \cdot \left( \frac{a}{2} \right)^{2}}{2} - площадь\ полукруга.\]

\[Площадь\ окна:\ \ \]

\[S = a \cdot 1,5a + \frac{\pi \cdot \left( \frac{a}{2} \right)^{2}}{2}.\]

\[если\ \ a = 80:\]

\[S = 80 \cdot 1,5 \cdot 80 + \frac{\pi}{2} \cdot \left( \frac{80}{2} \right)^{2} =\]

\[= 9600 + \frac{\pi}{2} \cdot (40)^{2} =\]

\[= 9600 + \frac{\pi}{2} \cdot 1600 =\]

\[= 9600 + \pi \cdot 800 =\]

\[= 9600 + 3,14 \cdot 800 =\]

\[= 9600 + 2512 = 12\ 112\ \left( см^{2} \right).\]

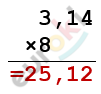
\[Ответ:S = 12112\ см^{2}.\]

\[\boxed{\text{407\ (407).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\text{\ x}^{6} = x \cdot x^{5}\]

\(\text{\ x}^{6} = x^{4} \cdot x^{2}\)

\[\text{\ x}^{6} = x^{3} \cdot x^{3}\]

\[\text{\ x}^{6} = x^{0} \cdot x^{6}\]

\[\text{\ x}^{6} = x^{6} \cdot x^{0}\]

\[\text{\ x}^{6} = x^{5} \cdot x\]

\[\text{\ x}^{6} = x^{2} \cdot x^{4}\]