Решебник по алгебре 7 класс Макарычев ФГОС Задание 1178

 

\[\boxed{\text{1178.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

\[\textbf{а)}\ \left\{ \begin{matrix} y + 3x = 0 \\ x - y = 4\ \ \\ x + y = - 2 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ }\]

\[\text{\ \ }\left\{ \begin{matrix} y = - 3x\ \ \ \ \ \\ y = x - 4\ \ \ \\ y = - 2 - x \\ \end{matrix} \right.\ \]

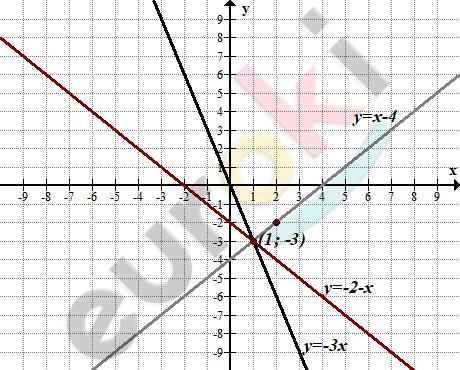
\[Решение:(1;\ - 3).\]

\[\textbf{б)}\ \left\{ \begin{matrix} x + y = 1\ \ \ \\ y - x = 3\ \ \\ 2x + y = 0 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ \ \ \ }\]

\[\text{\ \ }\left\{ \begin{matrix} y = 1 - x \\ y = 3 + x \\ y = - 2x\ \ \\ \end{matrix} \right.\ \]

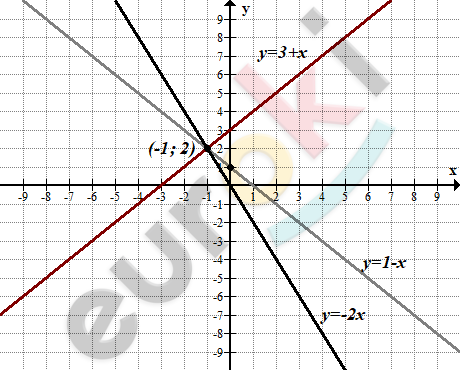
\[Решение:( - 1;2).\]

\[\boxed{\text{1178\ (1178).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Системой линейных уравнений называют два и более уравнения с несколькими переменными (буквы x, y и т.д.), для которых необходимо найти общее решение.

Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.

Алгоритм решения систем линейных уравнений способом сложения:

1. Умножить (разделить) левую и правую части одного или обоих уравнений на некоторое число так, чтобы коэффициенты (число перед буквой) при одной из переменных в разных уравнениях стали противоположными числами:

\[\left\{ \begin{matrix} \mathbf{x + y = 10\ \ | \bullet ( - 4)\ \ \ \ } \\ \mathbf{4}\mathbf{x + 5}\mathbf{y = 44\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} \mathbf{- 4}\mathbf{x}\mathbf{+}\left( \mathbf{- 4}\mathbf{y} \right)\mathbf{= - 40\ \ } \\ \mathbf{4}\mathbf{x}\mathbf{+ 5}\mathbf{y = 44\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \end{matrix} \right.\ \]

2. Сложить получившиеся уравнения почленно:

\[\left\{ \begin{matrix} \mathbf{- 4}\mathbf{x}\mathbf{+}\left( \mathbf{- 4}\mathbf{y} \right)\mathbf{=}\mathbf{- 40}\mathbf{\ } \\ \mathbf{4}\mathbf{x}\mathbf{+}\mathbf{5}\mathbf{y}\mathbf{=}\mathbf{44}\mathbf{\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ }} \\ \end{matrix} \right.\ ( + )\]

\[\left\{ \begin{matrix} \mathbf{y = 4\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \mathbf{4}\mathbf{x}\mathbf{+ 5}\mathbf{y = 44\ } \\ \end{matrix} \right.\ \]

3. Подставить полученное значение в одно из уравнений и найти значение второй переменной:

\[\mathbf{x + 4 = 10}\]

\[\mathbf{x = 10 - 4}\]

\[\mathbf{x = 6}\]

4. Записать решение:

(6; 4)

Свойства уравнений с двумя переменными:

1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;

2. Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то получится уравнение, равносильное данному.

Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.

Решение.

\[Пусть\ велосипедист\ ехал\ \]

\[от\ пункта\ \text{A\ }до\ \text{B\ x\ }часов,\ \]

\[а\ от\ пункта\ \text{B\ }до\ C\ y\ часов.\ \]

\[На\ весь\ путь\ он\ потратил\ \ \]

\[5\ часов.\ От\ A\ до\ \text{B\ }он\ ехал\ \]

\[со\ скоростью\ 10\ \frac{км}{ч},\ \ \ \]

\[а\ от\ \text{B\ }до\ C - 15\ \frac{км}{ч}.\]

\[Известно,\ что\ тот\ же\ путь\ за\ то\ \]

\[же\ время\ он\ мог\ проехать\ со\ \]

\[скоростью\ 12\ \frac{км}{ч}\mathbf{.}\]

\[\mathbf{Составим\ и\ решим\ систему\ }\]

\[\mathbf{уравнений:}\]

\[\left\{ \begin{matrix} x + y = 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 10x + 15y = 12 \cdot 5 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} x + y = 5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 10x + 15y = 60\ \ |\ :( - 10) \\ \end{matrix} \right.\ \]

\[Ответ:велосипедист\ затратил\ \]

\[3\ часа\ на\ путь\ от\ \text{A\ }до\ B;\]

\(и\ 2\ часа\ на\ путь\ от\ B\ до\ C.\)