Решебник по алгебре 7 класс Макарычев ФГОС Задание 1021

 

\[\boxed{\text{1021.}\text{\ }еуроки - ответы\ на\ пятёрку}\]

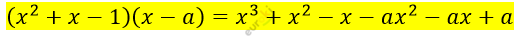
\[\textbf{а)}\ не\ содержит\ x²:\ \ \ \ \]

\[x^{2} - ax^{2} = 0\ \ \]

\[x^{2}(1 - a) = 0\ \]

\[a = 1.\]

\[\textbf{б)}\ не\ содержит\ \ x:\ \ \ \]

\[- x - ax = 0\ \]

\[- x(1 + a) = 0\]

\[a = - 1.\]

\[\boxed{\text{1021\ (1021).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

При решении используем следующее:

1. Формулу квадрата суммы:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

\[\mathbf{(}\mathbf{a}\mathbf{+}\mathbf{b}\mathbf{)}^{\mathbf{2}}\mathbf{=}\mathbf{a}^{\mathbf{2}}\mathbf{+}\mathbf{2}\mathbf{\text{ab}}\mathbf{+}\mathbf{b}^{\mathbf{2}}\mathbf{.}\]

2. Формулу квадрата разности:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения:

\[\mathbf{(}\mathbf{a}\mathbf{-}\mathbf{b}\mathbf{)}^{\mathbf{2}}\mathbf{=}\mathbf{a}^{\mathbf{2}}\mathbf{-}\mathbf{2}\mathbf{\text{ab}}\mathbf{+}\mathbf{b}^{\mathbf{2}}\mathbf{.}\]

3. Положительное или отрицательное число (со знаком «минус») во второй степени (квадрате) всегда будет числом положительным или 0:

\[\mathbf{( -}\mathbf{2)}^{\mathbf{2}}\mathbf{= 4;}\]

\[\mathbf{2}^{\mathbf{2}}\mathbf{= 4.}\]

Решение.

\[\textbf{а)}\ x² - 2xy + y^{2} + a^{2} =\]

\[= (x - y)^{2} + a^{2}\ \]

\[(x - y)^{2} \geq 0\ \ \ и\ \ \ a^{2} \geq 0 \Longrightarrow\]

\[\Longrightarrow (x - y)^{2} + a² \geq 0.\]

\[\textbf{б)}\ 4x² + a² - 4x + 1 =\]

\[= (2x - 1)^{2} + a^{2}\ \]

\[(2x - 1)^{2} \geq 0\ \ и\ \ \ a^{2} \geq 0 \Longrightarrow\]

\[\Longrightarrow (2x - 1)^{2} + a² \geq 0.\]

\[\textbf{в)}\ 9b² - 6b + 4c^{2} + 1 =\]

\[= (3b - 1)^{2} + 4c^{2}\ \]

\[(3b - 1)^{2} \geq 0\ \ и\ \ 4c^{2} \geq 0 \Longrightarrow\]

\[\Longrightarrow \ (3b - 1)^{2} + 4c² \geq 0.\]

\[\textbf{г)}\ a² + 2ab + 2b² + 2b + 1 =\]

\[= (a + b)^{2} + (b + 1)^{2},\]

\[(a + b)^{2} \geq 0\ \ \ и\ \ \ (b + 1)^{2} \geq 0\]

\[значит,\ \ \]

\[(a + b)^{2} + (b + 1)^{2} \geq 0.\]

\[\textbf{д)}\ x² - 4xy + y^{2} + x^{2}y^{2} + 1 =\]

\[= (x - y)^{2} + (xy - 1)^{2}\]

\[(x - y)^{2} \geq 0\ \ \ и\ \ \]

\[(xy - 1)^{2} \geq 0 \Longrightarrow\]

\[\Longrightarrow (x - y)^{2} + (xy - 1)^{2}.\]

\[\textbf{е)}\ x² + y² + 2x + 6y + 10 =\]

\[= (x + 1)^{2} + (y + 3)^{2}\text{\ \ }\]

\[(x + 1)^{2} \geq 0\ \ и\ \ \ (y + 3)^{2} \geq 0 \Longrightarrow\]

\[\Longrightarrow (x + 1)^{2} + (y + 3)^{2} \geq 0.\]