Решебник по алгебре 7 класс Рурукин контрольные работы КР-4. Степень с натуральным показателем Вариант 3

Условие:

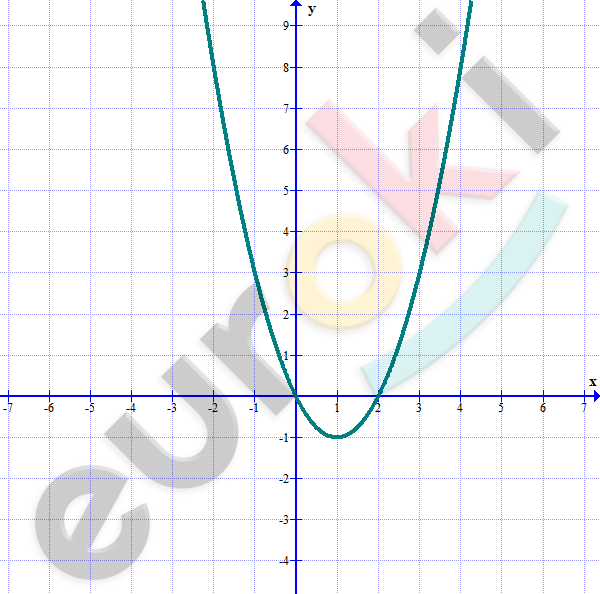
1. Дана функция y = x^2 − 2x. Составьте таблицу значений функции в промежутке −1 ≤ x ≤ 3 с шагом 0,5 и постройте график функции.

2. Выполните действия:

а) 3a^2 * 5a^3 * 2a^4 ;

б) a^18 : a^6 ;

в) (a^5 )^3 * (a^2 )^4 ;

г) (a^2 b*(ab^2 )^2)/(a^3 b^4 )

3. Запишите в виде одночлена стандартного вида выражение:

а) 5 * (xy^2 z^3 )^2 * (−2x^2 zy^3 )^3 ;

б) (2a^3 b^2 c^3 )^3 : (−3ac^2 b)^2 .

4. Сравните числа 2^30 и 3^20.

5. Решите уравнение:

а) ((x^8 )^3*(x^2 )^5)/((x^4 )^5*x^13 )=19

б) ((2^x )^2*2^7)/2^5 =16²

6. Докажите, что число 196^374 + 391^164 − 2 делится на 5.

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[y = x^{2} - 2x;\ \ - 1 \leq x \leq 3\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[\textbf{а)}\ 3a^{2} \cdot 5a^{3} \cdot 2a^{4} = 30a^{9}\]

\[\textbf{б)}\ a^{18}\ :a^{6} = a^{12}\]

\[\textbf{в)}\ \left( a^{5} \right)^{3} \cdot \left( a^{2} \right)^{4} = a^{15} \cdot a^{8} = a^{23}\]

\[\textbf{г)}\ \frac{a^{2}b \cdot \left( ab^{2} \right)^{2}}{a^{3}b^{4}} = \frac{a^{2}b \cdot a^{2}b^{4}}{a^{3}b^{4}} =\]

\[= \frac{a^{4}b^{5}}{a^{3}b^{4}} = ab\ \]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[\textbf{а)}\ 5 \cdot \left( xy^{2}z^{3} \right)^{2} \cdot \left( - 2x^{2}zy^{3} \right)^{3} =\]

\[= 5x^{2}y^{4}z^{6} \cdot \left( - 8x^{6}z^{3}y^{9} \right) =\]

\[= - 40x^{8}y^{13}z^{9}\]

\[\textbf{б)}\ \left( 2a^{3}b^{2}c^{3} \right)^{3}\ :\left( - 3ac^{2}b \right)^{2} =\]

\[= 8a^{9}b^{6}c^{9}\ :9a^{2}b^{2}c^{4} = \frac{8}{9}a^{7}b^{4}c^{5}\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[2^{30} < 3^{20}\]

\[2^{30} = 2^{3 \cdot 10} = 8^{10}\]

\[3^{20} = 3^{2 \cdot 10} = 9^{10}\]

\[9^{10} > 8^{10}.\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[\textbf{а)}\ \frac{\left( x^{8} \right)^{3} \cdot \left( x^{2} \right)^{5}}{\left( x^{4} \right)^{5} \cdot x^{13}} = 19\]

\[\frac{x^{24} \cdot x^{10}}{x^{20} \cdot x^{13}} = 19\]

\[\frac{x^{34}}{x^{33}} = 19\]

\[x = 19.\]

\[\textbf{б)}\ \frac{\left( 2^{x} \right)^{2} \cdot 2^{7}}{2^{5}} = 16^{2}\]

\[2^{2x} \cdot 2^{2} = 2^{8}\]

\[2^{2x} = 2^{6}\]

\[2x = 6\]

\[x = 3.\]

\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]

\[196^{374} + 391^{164} - 2\ \]

\[196^{374} - оканчивается\ на\ 6;\]

\[391^{164} - оканчивается\ на\ 1.\]

\[6 + 1 - 2 = 5 - делится\ на\ 5.\]

\[Что\ и\ требовалось\ доказать.\]