Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 7 класс Мерзляк контрольные работы КР-7. Системы линейных уравнений с двумя переменными Вариант 3
Вариант 3
Условие:
1. Решите методом подстановки систему уравнений:
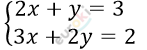
2. Решите методом сложения систему уравнений:
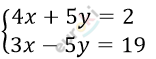
3. Решите графически систему уравнений:
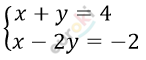
4. За 8 тетрадей и 5 ручек заплатили 171 р. Сколько стоит тетрадь и сколько стоит ручка, если 3 тетради дороже ручки на 21 р.?
5. Решите систему уравнений:
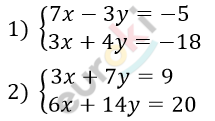
6. При каком значении a система уравнений имеет бесконечно много решений?
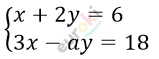
Решение:
\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]
\[\left\{ \begin{matrix} 2x + y = 3\ \ \\ 3x + 2y = 2 \\ \end{matrix} \right.\ \ \]
\[\left\{ \begin{matrix} y = 3 - 2x\text{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ 3x + 2 \cdot (3 - 2x) = 2 \\ \end{matrix} \right.\ \]
\[3x + 6 - 4x = 2\]
\[- x = - 4\]
\[x = 4.\]
\[y = 3 - 2 \cdot 4 = 3 - 8 = - 5.\]
\[\left\{ \begin{matrix} x = 4\ \ \ \\ y = - 5 \\ \end{matrix} \right.\ \]
\[Ответ:(4;\ - 5).\]
\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]
\[\left\{ \begin{matrix} 4x + 5y = 2\ \ \\ 3x - 5y = 19 \\ \end{matrix} \right.\ ( + )\text{\ \ \ \ \ \ }\]
\[7x = 21\]
\[x = 3.\]
\[\left\{ \begin{matrix} 5y = 2 - 4x \\ x = 3\ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \ \]
\[\left\{ \begin{matrix} x = 3\ \ \ \ \ \ \ \ \ \ \ \ \\ 5y = 2 - 12 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = 3\ \ \ \ \ \ \ \ \ \\ 5y = - 10 \\ \end{matrix} \right.\ \ \]
\[\left\{ \begin{matrix} x = 3\ \ \ \\ y = - 2 \\ \end{matrix} \right.\ \]
\[Ответ:(3;\ - 2).\]
\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]
\[\left\{ \begin{matrix} x + y = 4\ \ \ \ \ \ \\ x - 2y = - 2 \\ \end{matrix} \right.\ \ \]
\[\left\{ \begin{matrix} y = 4 - x\text{\ \ } \\ 2y = x + 2 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} y = 4 - x\text{\ \ \ \ \ \ } \\ y = 0,5x + 1 \\ \end{matrix} \right.\ \]
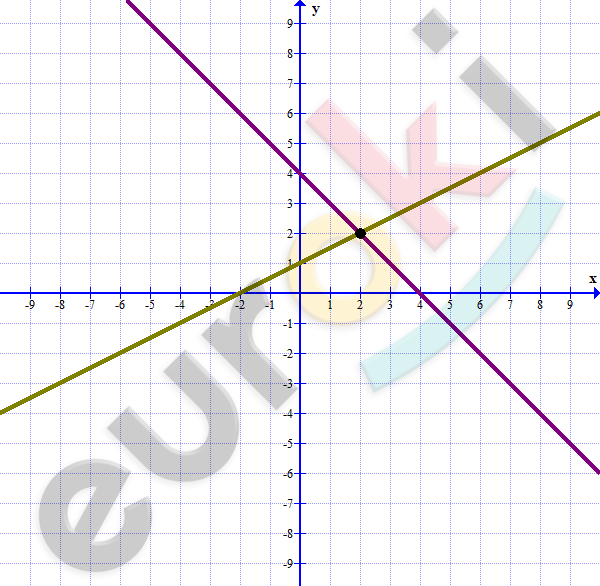
\[Ответ:(2;2).\]
\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]
\[Пусть\ \text{x\ }рублей - цена\ тетради,\]
\[тогда\ \text{y\ }рублей - цена\ ручки.\]
\[Составим\ систему\ уравнений:\]
\[\left\{ \begin{matrix} 8x + 5y = 171\ \ \ \ \ \ \ \\ 3x - y = 21\ \ \ | \cdot 5\ \ \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} 8x + 5y = 171\ \ \ \\ 15x - 5y = 105 \\ \end{matrix} \right.\ ( + )\]
\[23x = 276\]
\[x = 12\ (рублей) - цена\ \]
\[тетради.\]
\[y = 3x - 21 = 3 \cdot 12 - 21 =\]
\[= 36 - 21 = 15\ (рублей) -\]
\[цена\ ручки.\]
\[Ответ:12\ рублей\ и\ 15\ рублей.\]
\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]
\[1)\ \left\{ \begin{matrix} 7x - 3y = - 5\ \ \ \ | \cdot 4 \\ 3x + 4y = - 18\ \ | \cdot 3 \\ \end{matrix} \right.\ \text{\ \ \ \ \ \ \ }\]
\[\left\{ \begin{matrix} 28x - 12y = - 20 \\ 9x + 12y = - 54\ \ \ \\ \end{matrix} \right.\ ( + )\]
\[37x = - 74\]
\[x = - 2.\]
\[\left\{ \begin{matrix} x = - 2\ \ \ \ \ \ \ \ \ \\ 3y = 7x + 5 \\ \end{matrix} \right.\ \ \]
\[\left\{ \begin{matrix} x = - 2\ \ \ \ \ \ \ \ \ \ \ \ \ \\ 3y = - 14 + 5 \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} x = - 2\ \ \ \\ 3y = - 9 \\ \end{matrix} \right.\ \ \]
\[\left\{ \begin{matrix} x = - 2 \\ y = - 3 \\ \end{matrix} \right.\ \]
\[Ответ:( - 2; - 3).\]
\[2)\ \left\{ \begin{matrix} 3x + 7y = 9\ \ | \cdot 2\ \ \\ 6x + 14y = 20\ \ \ \ \ \ \\ \end{matrix} \right.\ \ \]
\[\left\{ \begin{matrix} 6x + 14y = 18 \\ 6x + 14y = 20 \\ \end{matrix} \right.\ \]
\[Система\ не\ имеет\ решений,\ \ \]
\[так\ как\ прямые\ параллельны.\]
\[Ответ:нет\ решений.\]
\[\boxed{\mathbf{6}\mathbf{.}\mathbf{\ }}\]
\[Система\ имеет\ бесконечно\ \ \]
\[много\ решений\ в\ том\ случае,\]
\[\ если\ прямые\ совпадают.\]
\[\left\{ \begin{matrix} x + 2y = 6\ \ \ \ | \cdot 3\ \\ 3x - \text{ay} = 18\ \ \ \ \ \ \ \\ \end{matrix} \right.\ \ \]
\[\left\{ \begin{matrix} 3x + 6y = 18 \\ 3x - \text{ay} = 18 \\ \end{matrix} \right.\ \]
\[a = - 6.\]
\[Ответ:при\ \ a = - 6.\]
