Решебник по алгебре 7 класс Мерзляк контрольные работы КР-6. Функции Вариант 2

Условие:

1. Функция задана формулой y = –2x + 3. Определите:
1) значение функции, если значение аргумента равно 3;
2) значение аргумента, при ко то ром значение функции равно 5;
3) проходит ли график функции через точку B (–1; 5).

2. Постройте график функции y = 5x – 4. Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно 1;
2) значение аргумента, при ко то ром значение функции равно 6.

3. Не выполняя построения, найдите координаты точек пересечения графика функции y = 0,2x – 10 с осями координат.

4. При каком значении k график функции y = kx – 15 проходит через точку C(-2;-3)?

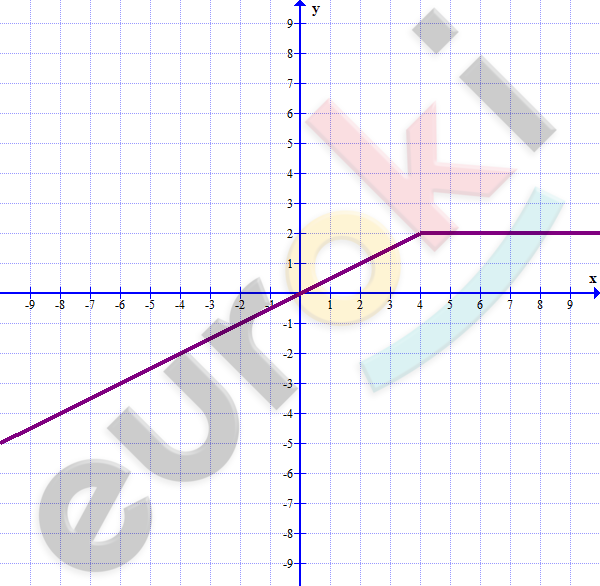
5. Постройте график функции: y=1/2*x; если x<=4; y=2; если x>4.

Решение:

\[\boxed{\mathbf{1}\mathbf{.}\mathbf{\ }}\]

\[y = - 2x + 3\]

\[1)\ x = 3 \rightarrow y = - 2 \cdot 3 + 3 =\]

\[= - 6 + 3 = - 3.\]

\[2)\ y = 5:\]

\[5 = - 2x + 3\]

\[- 2x = 2\]

\[x = - 1.\]

\[3)\ B( - 1;5):\]

\[5 = - 2 \cdot ( - 1) + 3\]

\[5 = 2 + 3\]

\[5 = 5 \rightarrow проходит.\]

\[\boxed{\mathbf{2}\mathbf{.}\mathbf{\ }}\]

\[y = 5x - 4\]

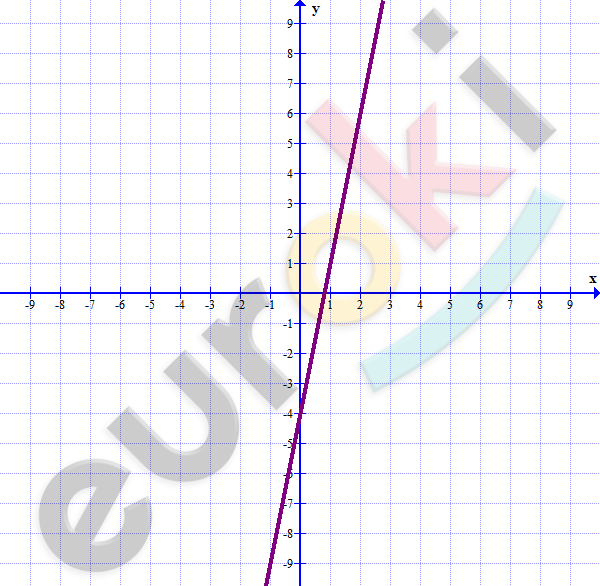
\[1)\ x = 1 \rightarrow y = 1.\]

\[2)\ y = 6 \rightarrow x = 2.\]

\[\boxed{\mathbf{3}\mathbf{.}\mathbf{\ }}\]

\[y = 0,2x - 10\]

\[Пересечение\ с\ осью\ \text{x\ }(y = 0):\]

\[0 = 0,2x - 10\]

\[0,2x = 10\]

\[x = 50.\]

\[Точка\ (50;0).\]

\[Пересечение\ с\ осью\ y\ (x = 0):\]

\[y = 0,2 \cdot 0 - 10 = - 10.\]

\[Точка\ (0; - 10).\]

\[\boxed{\mathbf{4}\mathbf{.}\mathbf{\ }}\]

\[y = kx - 15;\ \ \ C( - 2; - 3):\]

\[- 3 = - 2k - 15\]

\[- 2k = - 3 + 15\]

\[- 2k = 12\]

\[k = - 6.\]

\[Ответ:при\ k = - 6.\]

\[\boxed{\mathbf{5}\mathbf{.}\mathbf{\ }}\]

\[y = \left\{ \begin{matrix} \frac{1}{2}x;если\ x \leq 4 \\ 2;\ \ \ если\ x > 4 \\ \end{matrix} \right.\ \]