Решебник по алгебре 11 класс Никольский Параграф 8. Уравнения-следствия Задание 12

\[\boxed{\mathbf{12.}}\]

\[\sqrt{x^{2} + 6x - 2a} = x + 2\]

\[ОДЗ:\]

\[x + 2 \geq 0\]

\[x \geq - 2.\]

\[x^{2} + 6x - 2a = 0\]

\[D_{1} = 9 + 2a\]

\[x_{1} = - 3 + \sqrt{9 + 2a};\]

\[x_{2} = - 3 - \sqrt{9 + 2a};\]

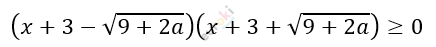
\[x \geq - 2.\]

\[x^{2} + 6x - 2a = (x + 2)^{2}\]

\[x^{2} + 6x - 2a = x^{2} + 4x + 4\]

\[2x - 2a = 4\]

\[2x = 2a + 4\]

\[x = a + 2.\]

\[x \geq - 2:\]

\[a + 2 \geq - 2\]

\[a \geq - 4.\]

\[Ответ:при\ a \geq - 4.\]