Решебник по алгебре 11 класс Никольский Параграф 6. Первообразная и интеграл Задание 71

\[\boxed{\mathbf{71}.}\]

\[\textbf{а)}\ y = 4 - 0,5x^{3};\]

\[y = 4 - 2x;\]

\[4 - 0,5x^{3} = 4 - 2x\]

\[2x - 0,5x^{3} = 0\]

\[- 0,5x\left( x^{2} - 4 \right) = 0\]

\[x = 0;\]

\[x = \pm 2.\]

\[y(0) = 4;\]

\[y(2) = 0;\]

\[y( - 2) = 8.\]

\[Площадь\ закрашенной\ фигуры\ \]

\[равны\ удвоенной\ разности\ \]

\[интегралов.\]

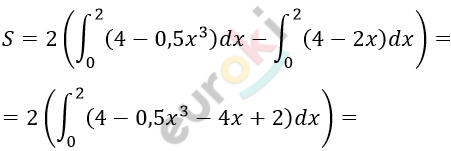
\[= 2\int_{0}^{2}{\left( - 0,5x^{3} + 2x \right)\text{dx}} =\]

\[= 2 \cdot (\left. \ - \frac{05}{4}x^{4} + x^{2}) \right|_{0}^{2} =\]

\[= 2 \cdot ( - 2 + 4 - 0) = 4\ кв.\ ед.\]

\[Ответ:\ 4\ кв.\ ед.\]

\[\textbf{б)}\ y = 0,5x^{3} + 8;\]

\[y = 2x + 8;\]

\[0,5x^{3} + 8 = 2x + 8\]

\[0,5x^{3} - 2x = 0\]

\[0,5x\left( x^{2} - 4 \right) = 0\]

\[x = 0;\]

\[x = \pm 2;\]

\[y(0) = 8;\]

\[y( - 2) = 4;\]

\[y(2) = 12.\]

\[Площадь\ закрашенной\ фигуры\ \]

\[равны\ удвоенной\ разности\ \]

\[интегралов.\]

\[= 2\int_{0}^{2}{\left( - 0,5x^{3} + 2x \right)\text{dx}} =\]

\[= 2 \cdot (\left. \ - \frac{05}{4}x^{4} + x^{2}) \right|_{0}^{2} =\]

\[= 2 \cdot ( - 2 + 4 - 0) = 4\ кв.\ ед.\]

\[Ответ:\ 4\ кв.\ ед\]