Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 11 класс Никольский Параграф 6. Первообразная и интеграл Задание 43
Задание 43
\[\boxed{\mathbf{43}.}\]
\[\textbf{а)}\ \int_{- 1}^{1}\text{xdx};\ \ \mathrm{\Delta}x = 0,2;\]
\[Разобьем\ отрезок\ \lbrack - 1;1\rbrack\ \]
\[с\ интервалом\ 0,2:\]
\[Из\ первого\ отрезка\ функции\ \]
\[\lbrack 0;1\rbrack\ берем\ значения\ \]
\[положительные;\]
\[из\ второго\ отрезка\ \lbrack - 1\ ;0\rbrack -\]
\[отрицательные.\]
\[\overline{S_{n}} =\]
\[= ( - 0,8 - 0,6 + \ldots + 1) \cdot 0,2 =\]
\[= 0,2;\]
\[=\]
\[= ( - 1 - 1,2 + \ldots + 0,8) \cdot 0,2 =\]
\[= - 0,2;\]
\[I = \frac{\overline{S_{n}} +}{2} = \frac{0,2 - 0,2}{2} = 0.\]
\[\textbf{б)}\ \int_{- 1}^{1}{x^{3}\text{dx}};\ \ \mathrm{\Delta}x = 0,2;\]
\[Разобьем\ отрезок\ \lbrack - 1;1\rbrack\ \]
\[с\ интервалом\ 0,2:\]
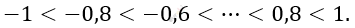
\[Из\ первого\ отрезка\ функции\ \]
\[\lbrack 0;1\rbrack\ берем\ значения\ \]
\[положительные;\]
\[из\ второго\ отрезка\ \lbrack - 1\ ;0\rbrack -\]
\[отрицательные.\]
\[\overline{S_{n}} =\]
\[= ( - 0,8 - 0,6 + \ldots + 1) \cdot 0,2 =\]
\[= 0,2;\]
\[=\]
\[= ( - 1 - 1,2 + \ldots + 0,8) \cdot 0,2 =\]
\[= - 0,2;\]
\[I = \frac{\overline{S_{n}} +}{2} = \frac{0,2 - 0,2}{2} =\]
\[\textbf{в)}\ \int_{- 1}^{1}\text{xdx};\ \ \mathrm{\Delta}x = 0,2;\]
\[Разобьем\ отрезок\ \lbrack - 1;1\rbrack\ \]
\[с\ интервалом\ 0,2:\]
\[Из\ первого\ отрезка\ функции\ \]
\[\lbrack 0;1\rbrack\ берем\ значения\ \]
\[положительные;\]
\[из\ второго\ отрезка\ \lbrack - 1\ ;0\rbrack -\]
\[отрицательные.\]
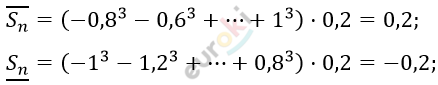
\[I = \frac{\overline{S_{n}} +}{2} = \frac{0,2 - 0,2}{2} = 0.\]
\[\textbf{г)}\ \int_{- \frac{\pi}{2}}^{\frac{\pi}{2}}{\sin x\text{dx}};\ \ \mathrm{\Delta}x = \frac{\pi}{20};\]
\[Разобьем\ отрезок\ \left\lbrack - \frac{\pi}{2};\frac{\pi}{2} \right\rbrack\ \]
\[с\ интервалом\ \frac{\pi}{20}:\]
\[Из\ первого\ отрезка\ функции\ \]
\[\left\lbrack 0;\frac{\pi}{2} \right\rbrack\ берем\ значения\ \]
\[положительные;\]
\[из\ второго\ отрезка\ \left\lbrack - \frac{\pi}{2}\ ;0 \right\rbrack -\]
\[отрицательные.\]
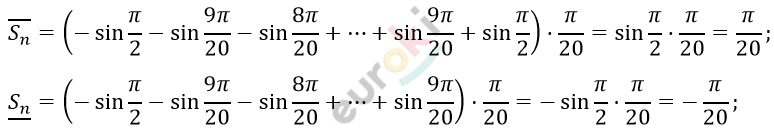
\[I = \frac{\overline{S_{n}} +}{2} = \frac{\frac{\pi}{20} - \frac{\pi}{20}}{2} = 0.\ \]
