Решебник по алгебре 11 класс Никольский Параграф 6. Первообразная и интеграл Задание 40

\[\boxed{\mathbf{40}.}\]

\[\textbf{а)}\ \int_{1}^{2}{2xdx};\ \ \int_{3}^{4}{3xdx}\]

\[\int_{1}^{2}{2xdx};\]

\[Разобьем\ отрезок\ \lbrack 1;2\rbrack\ \]

\[на\ 10\ частей:\]

\[1 < 1,1 < 1,2 < \ldots < 1,9 < 2.\]

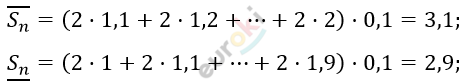
\[I = \frac{2,9 + 3,1}{2} = 3.\]

\[S = \frac{a + b}{2} \cdot h = \frac{2 + 4}{2} \cdot 1 = 3.\]

\[\int_{3}^{4}{3xdx};\]

\[Разделим\ отрезок\ \lbrack 3;4\rbrack\ \]

\[на\ 10\ частей:\]

\[3 < 3,1 < 3,2 < \ldots < 3,9 < 4.\]

\[I = \frac{10,65 + 10,35}{2} = \frac{21}{2} = 10,5.\]

\[S = \frac{a + b}{2} \cdot h = \frac{9 + 12}{2} \cdot 1 =\]

\[= 10,5.\]

\[Результаты\ вычислений\ \]

\[приближенно\ и\ как\ площади\ \]

\[одинаковы\ в\ обоих\ случаях.\]

\[\textbf{б)}\ Для\ линейной\ функции\ \]

\[приближенный\ метод\ \]

\[вычисления\ определенного\ \]

\[интеграла\ дает\ точный\ \]

\[результат,\ так\ как\ график\]

\[линейной\ функции - прямая,\ \]

\[и\ на\ каждом\ участке\ площадь\ \]

\[трапеции\ мы\ заменяем\ \]

\[на\ площадь\ той\ же\ самой\ \]

\[трапеции\ (без\ погрешностей).\]