Решебник по алгебре 11 класс Никольский Параграф 6. Первообразная и интеграл Задание 28

\[\boxed{\mathbf{28}.}\]

\[\textbf{а)}\ Интегральные\ суммы\ \]

\[отличаются\ только\ знаком.\]

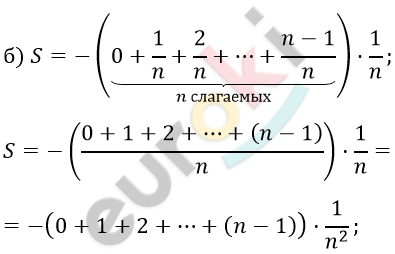
\[Сумма\ n\ первых\ членов\ \]

\[арифметической\ прогрессии\ \]

\[с\ разностью\ d = 1:\]

\[0;1;2;\ldots;n - 1;\]

\[S_{n} = \frac{a_{1} + a_{n}}{2} \cdot n =\]

\[= \frac{0 + (n - 1)}{2} \cdot n = \frac{n^{2} - n}{2};\]

\[\lim_{n \rightarrow \infty}S_{n} =\]

\[= \lim_{n \rightarrow \infty}S_{n}\left( - \frac{n^{2} - n}{2} \cdot \frac{1}{n^{2}} \right) =\]

\[= \lim_{n \rightarrow \infty}\left( - \frac{1 - \frac{1}{n}}{2} \right) =\]

\[= - \frac{1 - \lim_{n \rightarrow \infty}\frac{1}{n}}{2} =\]

\[= - \frac{1 - 0}{2} = - \frac{1}{2}.\]

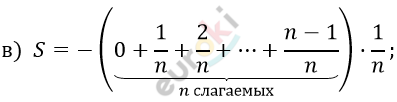
\[\lim_{n \rightarrow \infty}S_{n} = - \frac{1}{2};\]

\[y = - x;\ \ y = 0;\ \ x = 1:\]

\[Эта\ площадь\ равна\ \]

\[пределу\ \lim_{n \rightarrow \infty}S_{n} = - \frac{1}{2},\ \]

\[взятому\ со\ знаком\ минус:\]

\[S = \frac{1}{2}.\]