Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 11 класс Никольский Параграф 5. Применение производной Задание 58
Задание 58
\[\boxed{\mathbf{58.}}\]
\[\textbf{а)}\ y = \frac{x - 2,5}{x^{2} - 4};\ \ x \neq \pm 2\]
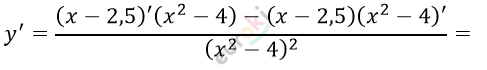
\[= \frac{x^{2} - 4 - 2x(x - 2,5)}{\left( x^{2} - 4 \right)^{2}} =\]
\[= \frac{x^{2} - 4 - 2x^{2} + 5x}{\left( x^{2} - 4 \right)^{2}} =\]
\[= \frac{- x^{2} + 5x - 4}{\left( x^{2} - 4 \right)^{2}};\]
\[- x^{2} + 5x - 4 = 0\]
\[x^{2} - 5x + 4 = 0\]
\[x_{1} + x_{2} = 5;\ \ \ x_{1} \cdot x_{2} = 4\]
\[x_{1} = 1;\ \ \ x_{2} = 4.\]
\[Критические\ точки:\]
\[x = 1;\ \ x = 4.\]
\[Функция\ возрастает:\]
\[1 \leq x < 2;\ \ 2 < x < 4.\]
\[Функция\ убывает:\]
\[x < - 2;\]
\[- 2 < x \leq 1;\]
\[x \geq 4.\]
\[\textbf{б)}\ y = \frac{x - 5}{9 - x^{2}};\ \ \ x \neq \pm 3\]
\[y^{'} = \frac{(x - 5)^{'}\left( 9 - x^{2} \right) - (x - 5)\left( 9 - x^{2} \right)^{'}}{\left( 9 - x^{2} \right)^{2}} =\]
\[= \frac{9 - x^{2} + 2x(x - 5)}{\left( 9 - x^{2} \right)^{2}} =\]
\[= \frac{9 - x^{2} + 2x^{2} - 10x}{\left( 9 - x^{2} \right)^{2}} =\]
\[= \frac{x^{2} - 10x + 9}{\left( 9 - x^{2} \right)^{2}};\]
\[x^{2} - 10x + 9 = 0\]
\[D_{1} = 25 - 9 = 16\]
\[x_{1} = 5 + 4 = 9;\]
\[x_{2} = 5 - 4 = 1.\]
\[Критические\ точки:\]
\[x = 1;\ \ x = 9.\]
\[Функция\ возрастает:\]
\[x < - 3;\ \ \ \]
\[- 3 < x \leq 1;\]
\[x \geq 9.\]
\[Функция\ убывает:\]
\[1 \leq x < 3;\]
\[3 < x \leq 9.\]
\[\textbf{в)}\ y = 2x^{2} - \ln x;\ \ x > 0\]
\[y^{'} = 4x - \frac{1}{x} = \frac{4x^{2} - 1}{x};\ \ x \neq 0\]
\[4x^{2} - 1 = 0\]
\[x^{2} = \frac{1}{4}\]
\[x = \pm \frac{1}{2}.\]
\[Критические\ точки:\]
\[x = \frac{1}{2}.\]
\[Функция\ возрастает:\]
\[x \geq \frac{1}{2}.\]
\[Функция\ убывает:\]
\[0 < x \leq \frac{1}{2}.\]
\[\textbf{г)}\ y = \ln x - 4,5x^{2};\ \ \ x > 0\]
\[y^{'} = \frac{1}{x} - 9x = \frac{1 - 9x^{2}}{x};\ \ x \neq 0\]
\[1 - 9x^{2} = 0\]
\[9x^{2} = 1\]
\[x^{2} = \frac{1}{9}\]
\[x = \pm \frac{1}{3}.\]
\[Критические\ точки:\]
\[x = \frac{1}{3}.\]
\[Функция\ возрастает:\]
\[0 < x \leq \frac{1}{3}.\]
\[Функция\ убывает:\]
\[x \geq \frac{1}{3}.\]
