Решебник по алгебре 11 класс Никольский Параграф 5. Применение производной Задание 117

\[\boxed{\mathbf{117}\mathbf{.}}\]

\[\textbf{а)}\ y = - x^{2}\left( 0,5x^{2} - 4 \right) =\]

\[= - 0,5x^{4} + 4x^{2};\]

\[D(f) = R;\]

\[функция\ четная;\]

\[x = 0;x = \pm 2 - критические\ \]

\[точки;\]

\[возрастает\ на\ ( - \infty; - 2)\ и\ \ \]

\[(0;2);\]

\[убывает\ на\ ( - 2;0)\ и\ (2; + \infty).\]

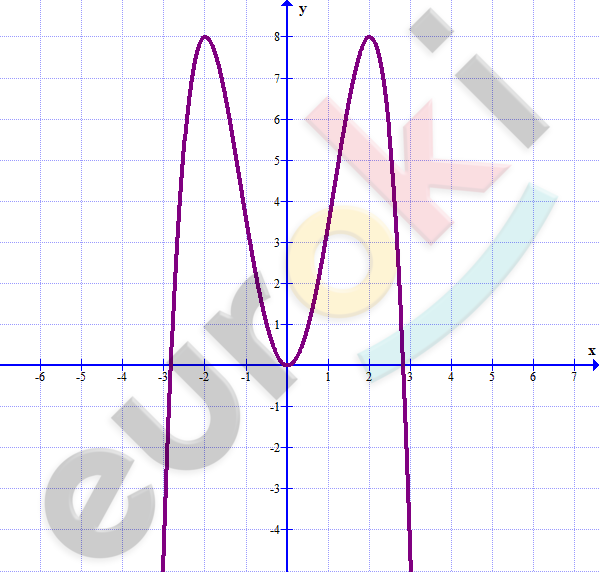
\[\textbf{б)}\ y = \left( x^{2} - 1 \right)^{2}\]

\[D(f) = R;\]

\[функция\ четная;\]

\[x = 0;x = \pm 1 - критические\ \]

\[точки;\]

\[убывает\ на\ ( - \infty; - 1)\ и\ \ (0;1);\]

\[возрастает\ на\ ( - 1;0)\ и\ \]

\[(1; + \infty).\]

\[\textbf{в)}\ y = - x + \frac{4}{3 - x} - 2 =\]

\[= \frac{- 3x + x^{2} + 4 - 6 + 2x}{3 - x} =\]

\[= \frac{x^{2} - x - 2}{3 - x};\]

\[D(f) \neq 3;\]

\[ни\ четная,\ ни\ нечетная;\]

\[y = - x - 2 \rightarrow наклонная\ \]

\[асимптота;\]

\[x = 3 - вертикальная\ \]

\[асимптота;\]

\[x = 1;x = 5 - критические\ \]

\[точки;\]

\[возрастает\ на\ (1;3)\ и\ (3;5);\]

\[убывает\ на\ ( - \infty;1)\ и\ (5; + \infty);\]

\[выпукла\ вниз\ на\ ( - \infty;3);\]

\[выпукла\ вверх\ на\ (3; + \infty).\]

\[\textbf{г)}\ y = x + \frac{1}{x - 1} - 3 =\]

\[= \frac{x^{2} - x + 1 - 3x + 3}{x - 1} =\]

\[= \frac{x^{2} - 4x + 4}{x - 1} = \frac{(x - 2)^{2}}{x - 1};\]

\[D(f) \neq 1;\]

\[ни\ четная,\ ни\ нечетная;\]

\[y = x - 3 \rightarrow наклонная\ \]

\[асимптота;\]

\[x = 1 - вертикальная\ \]

\[асимптота;\]

\[x = 2;x = 0 - критические\ \]

\[точки;\]

\[убывает\ на\ (0;1)\ и\ (1;2);\]

\[возрастает\ на\ ( - \infty;0)\ и\ \]

\[(2; + \infty);\]

\[выпукла\ вниз\ на\ (1; + \infty);\]

\[выпукла\ вверх\ на\ ( - \infty;1).\]

\[\textbf{д)}\ y = \frac{x^{2} - 4}{x^{2} + 1};\]

\[D(f) = R;\]

\[четная;\]

\[y = 1 \rightarrow горизонтальная\ \]

\[асимптота;\]

\[x = 0 - критические\ точки;\]

\[убывает\ на\ ( - \infty;0);\]

\[возрастает\ на\ (0; + \infty);\]

\[x = \pm \frac{1}{\sqrt{3}} - точки\ перегиба;\]

\[выпукла\ вниз\ на\ \left( - \frac{1}{\sqrt{3}};\frac{1}{\sqrt{3}} \right);\]

\[выпукла\ вверх\ на\ \left( - \infty; - \frac{1}{\sqrt{3}} \right);\]

\[\left( \frac{1}{\sqrt{3}}; + \infty \right).\]

\[\textbf{е)}\ y = \frac{x^{2} - 4}{x^{2} + 4};\]

\[D(f) = R;\]

\[четная;\]

\[y = 1 \rightarrow горизонтальная\ \]

\[асимптота;\]

\[x = 0 - критические\ точки;\]

\[убывает\ на\ ( - \infty;0);\]

\[возрастает\ на\ (0; + \infty);\]

\[x = \pm \frac{2}{\sqrt{3}} - точки\ перегиба;\]

\[выпукла\ вниз\ на\ \left( - \frac{2}{\sqrt{3}};\frac{2}{\sqrt{3}} \right);\]

\[выпукла\ вверх\ на\ \left( - \infty; - \frac{2}{\sqrt{3}} \right);\]

\[\left( \frac{2}{\sqrt{3}}; + \infty \right).\]

\[\textbf{ж)}\ y = \frac{x^{2} - 4}{x^{2} - 1};\]

\[четная;\]

\[y = 1 \rightarrow горизонтальная\ \]

\[асимптота;\]

\[x = \pm 1 - вертикальные\ \]

\[асимптоты;\]

\[x = 0 - критические\ точки;\]

\[убывает\ на\ ( - \infty; - 1)\ и\ ( - 1;0);\]

\[возрастает\ на\ (0;1)\ и\ (1;\ + \infty);\]

\[точек\ перегиба\ нет;\]

\[выпукла\ вниз\ на\ ( - 1;1);\]

\[выпукла\ вверх\ на\ ( - \infty; - 1);\]

\[(1; + \infty).\]

\[\textbf{з)}\ y = \frac{x^{2} + 1}{x^{2} - 1};\]

\[четная;\]

\[y = 1 \rightarrow горизонтальная\ \]

\[асимптота;\]

\[x = \pm 1 - вертикальные\ \]

\[асимптоты;\]

\[x = 0 - критические\ точки;\]

\[возрастает\ на\ ( - \infty; - 1)\ и\ \]

\[( - 1;0);\]

\[убывает\ на\ (0;1)\ и\ (1;\ + \infty);\]

\[точек\ перегиба\ нет;\]

\[выпукла\ вверх\ на\ ( - 1;1);\]

\[выпукла\ вниз\ на\ ( - \infty; - 1);\]

\[(1; + \infty).\]