Решебник по алгебре 11 класс Никольский Параграф 5. Применение производной Задание 115

\[\boxed{\mathbf{115}\mathbf{.}}\]

\[\textbf{а)}\ y = - 2x^{4} + 4x^{2} + 3;\ \ \]

\[\lbrack - 2;0,5\rbrack\]

\[y^{'} = - 8x^{3} + 8x;\]

\[- 8x^{3} + 8x = 0\]

\[- 8x\left( x^{2} - 1 \right) = 0\]

\[x = 0;x = \pm 1.\]

\[Возрастает\ при\ ( - \infty; - 1\rbrack\ и\ \]

\[\lbrack 0;1\rbrack;\]

\[убывает\ при\ \lbrack - 1;0\rbrack\ и\ \lbrack 1; + \infty).\]

\[y(0) = 3;\]

\[y( - 1) = 5;\]

\[y(1) = 5.\]

\[Точки\ экстремума:\]

\[( - 1;5);(0;3);(1;5).\]

\[y( - 2) = - 13;\]

\[y(0,5) = 3\frac{7}{8};\]

\[y_{наим} = - 13;\]

\[y_{наиб} = 5.\]

\[\textbf{б)}\ y = x^{3} - 3x + 3;\ \ \lbrack - 0,5;3\rbrack\]

\[y^{'} = 3x^{2} - 3;\]

\[3x^{2} - 3 = 0\]

\[3\left( x^{2} - 1 \right) = 0\]

\[x = \pm 1.\]

\[Возрастает\ при\ ( - \infty; - 1\rbrack\ и\ \]

\[\lbrack 1; + \infty);\]

\[убывает\ при\ \lbrack - 1;1\rbrack\text{\ .}\]

\[x = \pm 1 \rightarrow точки\ экстремума.\]

\[y(1) = 1;\]

\[y( - 0,5) = 4\frac{3}{8};\]

\[y(3) = 21.\]

\[y_{наим} = 1;\]

\[y_{наиб} = 21.\]

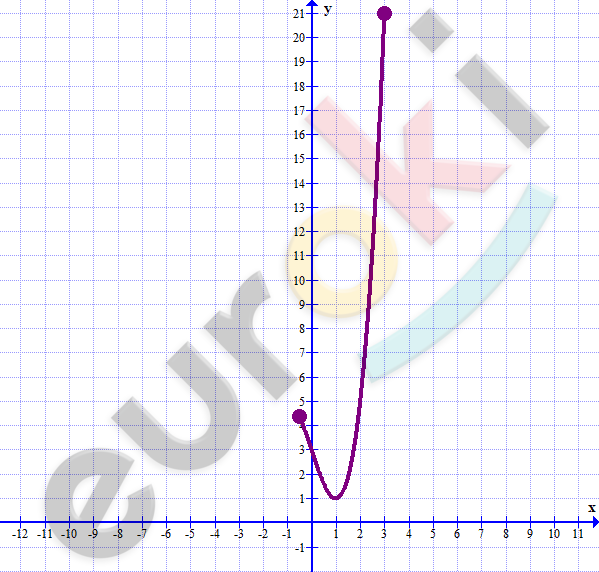
\[\textbf{в)}\ y = (x - 1)^{2}(2x + 4);\ \ \]

\[\lbrack - 2,5;1,5\rbrack\]

\[6x^{2} - 6 = 0\]

\[x^{2} = 1\]

\[x = \pm 1.\ \]

\[Возрастает\ при\ ( - \infty; - 1\rbrack\ и\ \]

\[\lbrack 1; + \infty);\]

\[убывает\ при\ \lbrack - 1;1\rbrack\text{\ .}\]

\[x = \mp 1 \rightarrow точки\ экстремума.\]

\[y( - 2,5) = - 12,25;\]

\[y( - 1) = 8;\]

\[y(1) = 0;\]

\[y(1,5) = 1,75.\]

\[y_{наим} = - 12,25;\]

\[y_{наиб} = 8.\]

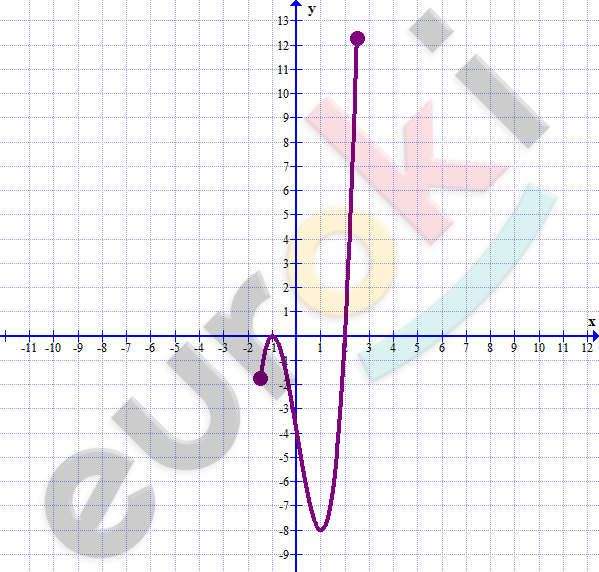
\[\textbf{г)}\ y = (2x - 4)(x + 1)^{2} =\]

\[= (2x - 4)\left( x^{2} + 2x + 1 \right) =\]

\[= 2x^{3} - 6x - 4;\ \ \lbrack - 1,5;2,5\rbrack\]

\[y^{'} = 6x^{2} - 6;\]

\[6x^{2} - 6 = 0\]

\[x^{2} = 1\]

\[x = \pm 1.\]

\[Возрастает\ при\ ( - \infty; - 1\rbrack\ и\ \]

\[\lbrack 1; + \infty);\]

\[убывает\ при\ \lbrack - 1;1\rbrack\text{\ .}\]

\[x = \pm 1 \rightarrow точки\ экстремума.\]

\[y(2,5) = 12,25;\]

\[y(1) = - 8;\]

\[y( - 1) = 0;\]

\[y( - 1,5) = - 1,75.\]

\[y_{наим} = - 8;\]

\[y_{наиб} = 12,25.\]

\[\textbf{д)}\ y = \frac{1}{8}(x + 3)(x - 3)^{2};\lbrack - 2;1\rbrack\]

\[= \frac{1}{8}(x - 3)(3x + 3) =\]

\[= \frac{3}{8}(x - 3)(x + 1);\]

\[\frac{3}{8}(x - 3)(x + 1) = 0\]

\[x = 3;x = - 11\]

\[Возрастает\ при\ ( - \infty; - 1\rbrack\ и\ \]

\[\lbrack 3; + \infty);\]

\[убывает\ при\ \lbrack - 1;3\rbrack\text{\ .}\]

\[x = - 1;x = 3 \rightarrow точки\ \]

\[экстремума.\]

\[y( - 2) = 3\frac{1}{8};\]

\[y( - 1) = 4;\]

\[y(1) = 2.\]

\[y_{наим} = 2;\]

\[y_{наиб} = 4.\]

\[\textbf{е)}\ y = \frac{1}{4}(x - 3)(x + 3)^{2};\]

\[\lbrack - 4; - 1\rbrack\]

\[= \frac{1}{4}(x + 3)^{2} + \frac{1}{2}(x + 3)(x - 3) =\]

\[= \frac{1}{4}(x + 3)(3x - 3) =\]

\[= \frac{3}{4}(x + 3)(x - 1);\]

\[\frac{3}{4}(x + 3)(x - 1) = 0\]

\[x = - 3;\ \ x = 1.\]

\[Возрастает\ при\ ( - \infty; - 3\rbrack\ и\ \]

\[\lbrack 1; + \infty);\]

\[убывает\ при\ \lbrack - 3;1\rbrack\text{\ .}\]

\[x = - 3;x = 1 \rightarrow точки\ \]

\[экстремума.\]

\[y( - 4) = - 1б75;\]

\[y( - 3) = 0;\]

\[y( - 1) = - 4.\]

\[y_{наим} = - 4;\]

\[y_{наиб} = 0.\]