Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 11 класс Никольский Параграф 5. Применение производной Задание 114
Задание 114
\[\boxed{\mathbf{114}\mathbf{.}}\]
\[\textbf{а)}\ y = x^{3} - 3x^{2} - 1;\]
\[определена\ и\ непрерывна\ \]
\[для\ всех\ x.\]
\[f^{'}(x) = 3x^{2} - 6x;\]
\[f^{'}(x) = 0:\]
\[3x^{2} - 6x = 0\]
\[3x(x - 2) = 0\]
\[критические\ точки:\]
\[x = 0;x = 2.\]
\[f(0) = - 1;\]
\[f(2) = - 5.\]
\[Точки\ экстремума:\]
\[(0; - 1);\ (2; - 5).\]
\[Промежутки\ возрастания:\]
\[x \leq 0;\ \]
\[x \geq 2.\]
\[Промежутки\ убывания:\]
\[0 \leq x \leq 2.\]
\[\textbf{б)}\ y = x^{4} - 2x^{2} + 3;\]
\[определена\ и\ непрерывна\ \]
\[для\ всех\ x.\]
\[f^{'}(x) = 4x^{3} - 4x;\]
\[f^{'}(x) = 0:\]
\[4x^{3} - 4x = 0\]
\[4x(x^{2} - 1) = 0\]
\[критические\ точки:\]
\[x = 0;x = \pm 1.\]
\[f(0) = 3;\]
\[f(1) = 2;\]
\[f( - 1) = 2.\]
\[Точки\ экстремума:\]
\[(0;3);\ \ (1;2);\ \ ( - 1;2).\]
\[Промежутки\ возрастания:\]
\[- 1 \leq x \leq 0;\ \]
\[x \geq 1.\]
\[Промежутки\ убывания:\]
\[x \leq - 1;\]
\[0 \leq x \leq 1.\]
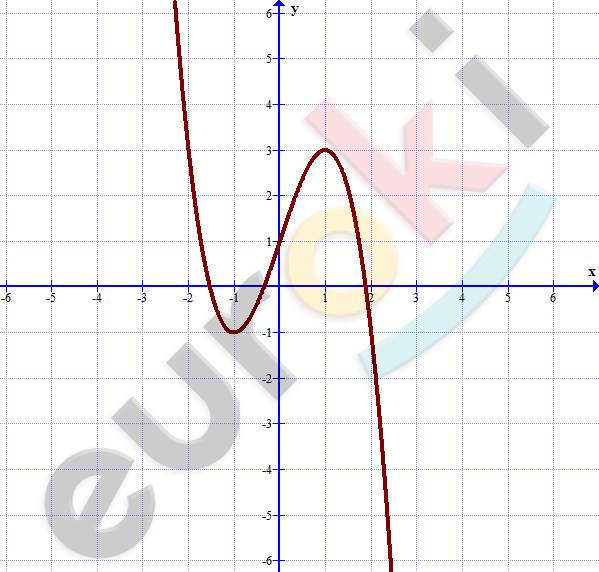
\[\textbf{в)}\ y = - x^{3} + 3x + 1;\]
\[определена\ и\ непрерывна\ \]
\[для\ всех\ x.\]
\[f^{'}(x) = - 3x^{2} + 3;\]
\[f^{'}(x) = 0:\]
\[- 3x^{2} + 3 = 0\]
\[- 3x^{2} = - 3\]
\[x^{2} = 1\]
\[x = \pm 1.\]
\[критические\ точки:\]
\[x = \pm 1.\]
\[f(1) = 3;\]
\[f( - 1) = - 1.\]
\[Точки\ экстремума:\]
\[(1;3);\ \ ( - 1; - 1).\]
\[Промежутки\ возрастания:\]
\[- 1 \leq x \leq 1.\ \]
\[Промежутки\ убывания:\]
\[x \leq - 1;\]
\[x \geq 1.\]
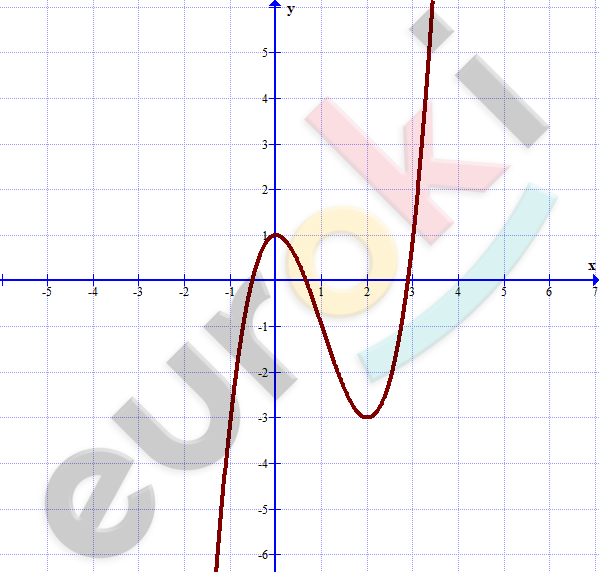
\[\textbf{г)}\ y = x^{3} - 3x^{2} + 1;\]
\[определена\ и\ непрерывна\ \]
\[для\ всех\ x.\]
\[f^{'}(x) = 3x^{2} - 6x;\]
\[f^{'}(x) = 0:\]
\[3x^{2} - 6x = 0\]
\[3x(x - 2) = 0\]
\[x = 0;x = 2.\]
\[критические\ точки:\]
\[x = 0;\ \ x = 1.\]
\[f(0) = 1;\]
\[f(2) = - 3.\]
\[Точки\ экстремума:\]
\[(0;1);\ \ (2; - 3).\]
\[Промежутки\ возрастания:\]
\[x \leq 0;\]
\[x \geq 2.\ \]
\[Промежутки\ убывания:\]
\[0 \leq x \leq 2.\]
\[\textbf{д)}\ y = \frac{1}{3}x^{3} - 3x^{2} + 5x + 1;\]
\[определена\ и\ непрерывна\ \]
\[для\ всех\ x.\]
\[f^{'}(x) = x^{2} - 6x + 5;\]
\[f^{'}(x) = 0:\]
\[x^{2} - 6x + 5 = 0\]
\[D_{1} = 9 - 5 = 4\]
\[x_{1} = 3 + 2 = 5;\]
\[x_{2} = 3 - 2 = 1.\]
\[критические\ точки:\]
\[x = 5;\ \ x = 1.\]
\[f(5) = - 7\frac{1}{3};\]
\[f(1) = 3\frac{1}{3}.\]
\[Точки\ экстремума:\]
\[\left( 1;3\frac{1}{3} \right);\ \ \left( 5;\ - 7\frac{1}{3} \right).\]
\[Промежутки\ возрастания:\]
\[x \leq 1;\]
\[x \geq 5.\ \]
\[Промежутки\ убывания:\]
\[1 \leq x \leq 5.\]
\[\textbf{е)}\ y = \frac{1}{3}x^{3} + 3x^{2} - 7x - 2;\]
\[определена\ и\ непрерывна\ \]
\[для\ всех\ x.\]
\[f^{'}(x) = x^{2} + 6x - 7;\]
\[f^{'}(x) = 0:\]
\[x^{2} + 6x - 7 = 0\]
\[D_{1} = 9 + 7 = 16\]
\[x_{1} = - 3 + 4 = 1;\]
\[x_{2} = - 3 - 4 = - 7.\]
\[критические\ точки:\]
\[x = - 7;\ \ x = 1.\]
\[f( - 7) = 79\frac{2}{3};\]
\[f(1) = - 5\frac{2}{3}.\]
\[Точки\ экстремума:\]
\[\left( 1; - 5\frac{2}{3} \right);\ \ \left( - 7;\ 79\frac{2}{3} \right).\]
\[Промежутки\ возрастания:\]
\[x \leq - 7;\]
\[x \geq 1.\ \]
\[Промежутки\ убывания:\]
\[- 7 \leq x \leq 1.\]
