Решебник по алгебре 11 класс Никольский Параграф 5. Применение производной Задание 112

\[\boxed{\mathbf{112}\mathbf{.}}\]

\[\textbf{а)}\ y = \frac{- 3x - 1}{x + 1};\]

\[\frac{- 3x - 1}{x + 1} = \frac{- 3(x + 1) + 3 - 1}{x + 1} =\]

\[= \frac{- 3(x + 1)}{x + 1} + \frac{2}{x + 1} =\]

\[= \frac{2}{x + 1} - 3;\]

\[Асимптоты:\]

\[y = - 3;\ \ x = - 1.\]

\[\textbf{б)}\ y = \left| \frac{- 3x - 1}{x + 1} \right|;\]

\[\frac{- 3x - 1}{x + 1} = \frac{- 3(x + 1) + 3 - 1}{x + 1} =\]

\[= \frac{- 3(x + 1)}{x + 1} + \frac{2}{x + 1} =\]

\[= \frac{2}{x + 1} - 3;\]

\[Асимптоты:\]

\[y = - 3;\ \ x = - 1.\]

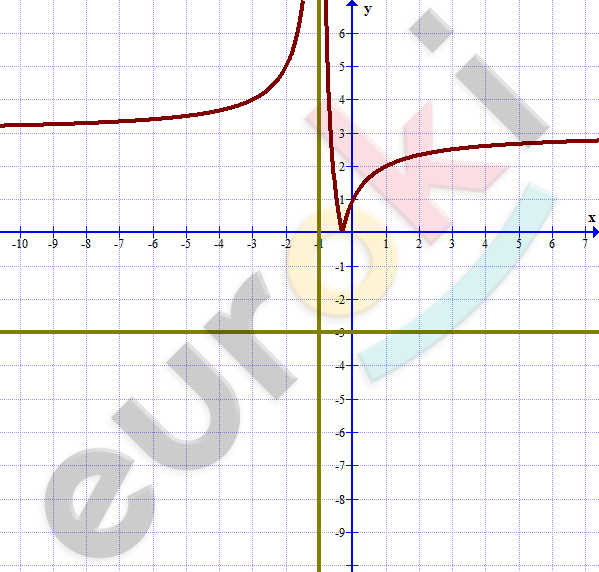
\[\textbf{в)}\ y = \frac{- 3|x| - 1}{|x| + 1};\]

\[\frac{- 3x - 1}{x + 1} = \frac{- 3(x + 1) + 3 - 1}{x + 1} =\]

\[= \frac{- 3(x + 1)}{x + 1} + \frac{2}{x + 1} =\]

\[= \frac{2}{x + 1} - 3;\]

\[Асимптоты:\]

\[y = - 3;\ \ x = - 1.\]

\[\textbf{г)}\ y = \left| \frac{- 3|x| - 1}{|x| + 1} \right|;\]

\[\frac{- 3x - 1}{x + 1} = \frac{- 3(x + 1) + 3 - 1}{x + 1} =\]

\[= \frac{- 3(x + 1)}{x + 1} + \frac{2}{x + 1} =\]

\[= \frac{2}{x + 1} - 3;\]

\[Асимптоты:\]

\[y = - 3;\ \ x = - 1.\]