Решебник по алгебре 11 класс Никольский Параграф 3. Обратные функции Задание 9

\[\boxed{\mathbf{9}\mathbf{.}}\]

\[\textbf{а)}\ y = \sqrt{4 - x^{2}};\ \ x \in \lbrack - 2;0\rbrack\]

\[4 - x^{2} = y^{2}\]

\[x^{2} = 4 - y^{2}\]

\[x = \pm \sqrt{4 - y^{2}}\]

\[y = - \sqrt{4 - x^{2}};\ \ x \in \lbrack 0;2\rbrack.\]

\[\textbf{б)}\ y = \sqrt{4 - x^{2}};\ \ x \in \lbrack 0;2\rbrack\]

\[4 - x^{2} = y^{2}\]

\[x^{2} = 4 - y^{2}\]

\[x = \pm \sqrt{4 - y^{2}}\]

\[y = \sqrt{4 - x^{2}};\ \ x \in \lbrack 0;2\rbrack.\]

\[\textbf{в)}\ y = \sqrt{21 - x^{2} + 4x};\ \ \]

\[x \in \lbrack - 3;2\rbrack\]

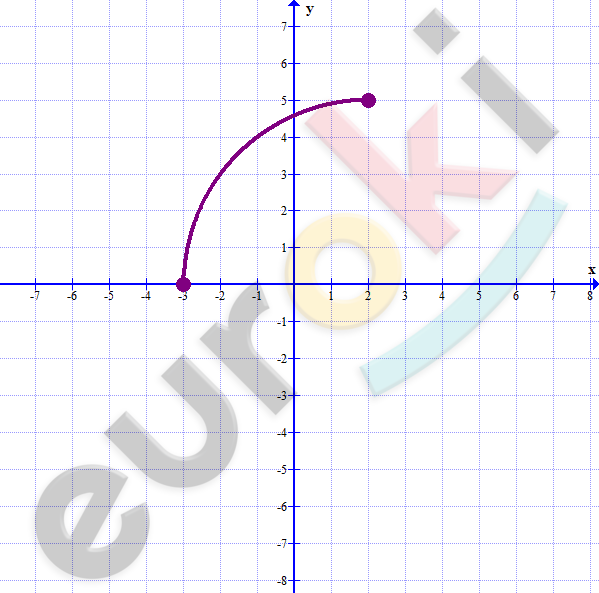
\[- x^{2} + 4x + 21 = y^{2}\]

\[x^{2} - 4x - 21 = - y^{2}\]

\[\left( x^{2} - 4x + 4 \right) - 25 = - y^{2}\]

\[(x - 2)^{2} = 25 - y^{2}\]

\[x - 2 = \pm \sqrt{25 - y^{2}}\]

\[x = \pm \sqrt{25 - y^{2}} + 2\]

\[y = - \sqrt{25 - x^{2}} + 2;\ \ x \in \lbrack 0;5\rbrack.\]

\[\textbf{г)}\ y = 4 + \sqrt{16 - x^{2} + 6x};\ \ \]

\[x \in \lbrack 3;8\rbrack\]

\[- x^{2} + 6x + 16 = (y - 4)^{2}\]

\[x^{2} - 6x + 9 - 25 = - (y - 4)^{2}\]

\[(x - 3)^{2} = 25 - (y - 4)^{2}\]

\[x - 3 = \pm \sqrt{25 - (y - 4)^{2}}\]

\[x = \pm \sqrt{25 - (y - 4)^{2}} + 3\]

\[y = \sqrt{25 - (x - 4)^{2}} + 3;\ \]

\[\ x \in \lbrack 4;9\rbrack.\]

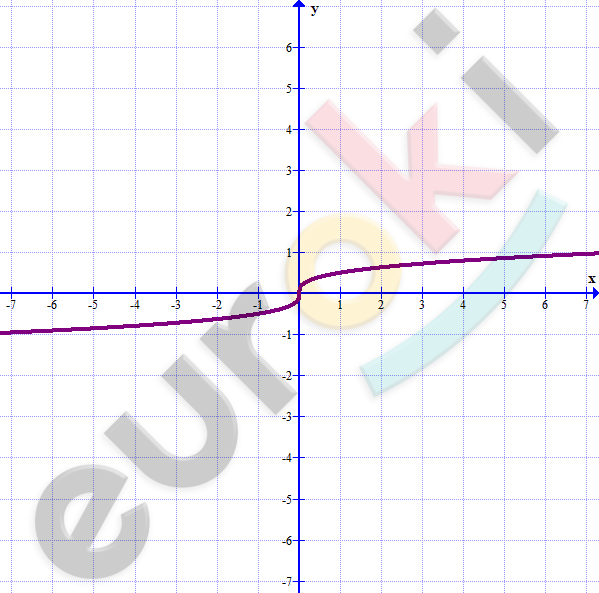
\[\textbf{д)}\ y = 8x^{3};\ \ \ X = R\]

\[x^{3} = \frac{y}{8}\]

\[x = \sqrt[3]{\frac{y}{8}} = \frac{1}{2}\sqrt[3]{y}\]

\[y = \frac{1}{2}\sqrt[3]{x}.\]

\[\textbf{е)}\ y = 0,5\sqrt{x};\ \ x \geq 0\]

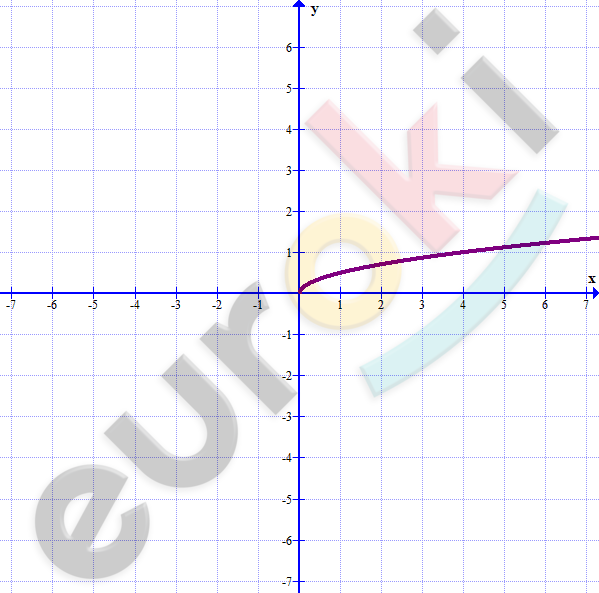
\[\sqrt{x} = \frac{y}{0,5} = 2y\]

\[x = 4y^{2}\]

\[y = 4x^{2};\ \ x \geq 0.\]

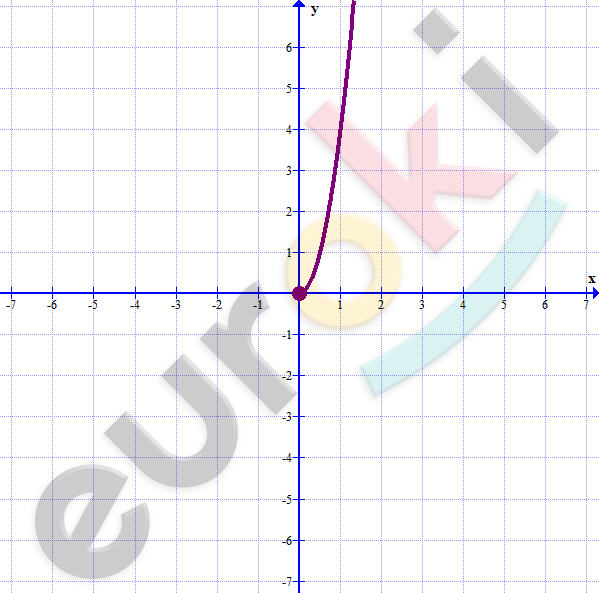
\[\textbf{ж)}\ y = 3^{x - 1}\]

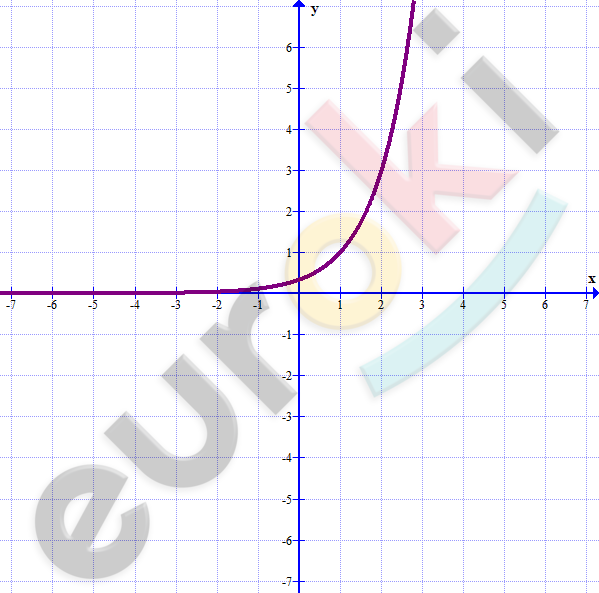
\[x - 1 = \log_{3}y\]

\[x = \log_{3}y + 1\]

\[y = \log_{3}x + 1;\ \ x > 0.\]

\[\textbf{з)}\ y = \left( \frac{1}{3} \right)^{x - 1}\]

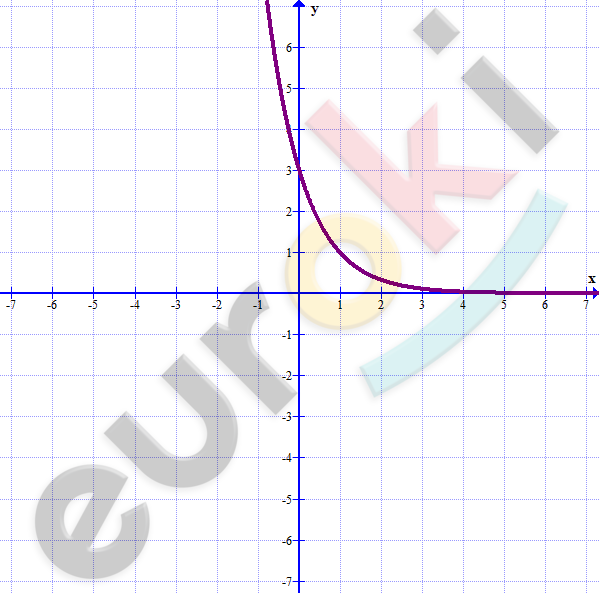
\[x - 1 = \log_{\frac{1}{3}}y\]

\[x = \log_{\frac{1}{3}}y + 1\]

\[y = \log_{\frac{1}{3}}x + 1;\ \ x > 0.\]

\[\textbf{и)}\ y = \log_{5}{(x + 2)}\]

\[x + 2 = 5^{y}\]

\[x = 5^{y} - 2\]

\[y = 5^{x} - 2;\ \ X = R.\]

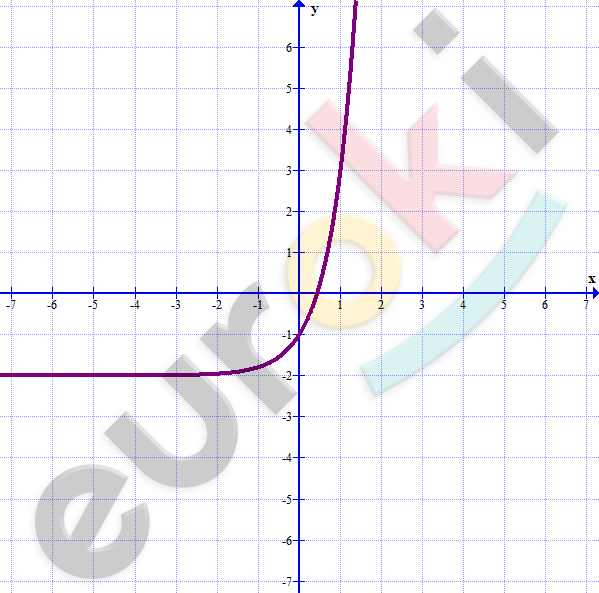
\[к)\ y = \log_{0,2}{(x - 1)}\ \]

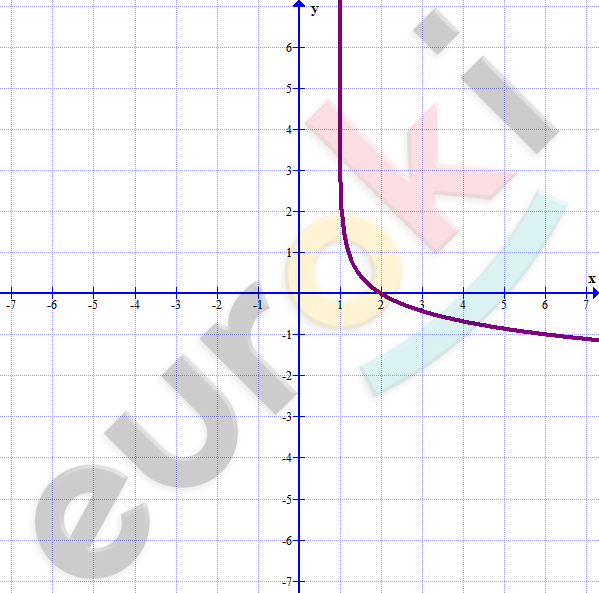
\[x - 1 = (0,2)^{y}\]

\[x = (0,2)^{y} + 1\]

\[y = (0,2)^{x} + 1;\ \ X = R.\]