Решебник по алгебре 11 класс Никольский Параграф 3. Обратные функции Задание 8

\[\boxed{\mathbf{8}\mathbf{.}}\]

\[\textbf{а)}\ y = \frac{4}{x - 2};\ \ x \in (2; + \infty)\]

\[x - 2 = \frac{4}{y}\]

\[x = \frac{4}{y} + 2\]

\[y = \frac{4}{x} + 2;y \in (2; + \infty) -\]

\[обратная\ функция.\]

\[\textbf{б)}\ y = \frac{- 4}{x - 2};\ \ x \in ( - \infty;2)\]

\[x - 2 = - \frac{4}{y}\]

\[x = - \frac{4}{y} + 2\]

\[y = - \frac{4}{x} + 2;y \in ( - \infty;2) -\]

\[обратная\ функция.\]

\[\textbf{в)}\ y = 1 - \frac{6}{x + 2} = \frac{- 6}{x + 2} + 1;\ \]

\[\ x \in ( - 2; + \infty)\]

\[- \frac{6}{x + 2} = y - 1\]

\[x + 2 = - \frac{6}{y - 1}\]

\[x = - \frac{6}{y - 1} - 2\]

\[y = \frac{- 6}{x - 1} - 2;\ \ y \in ( - 2;\ + \infty).\]

\[\textbf{г)}\ y = 1 + \frac{6}{x - 4};\ \ x \in ( - \infty;4)\]

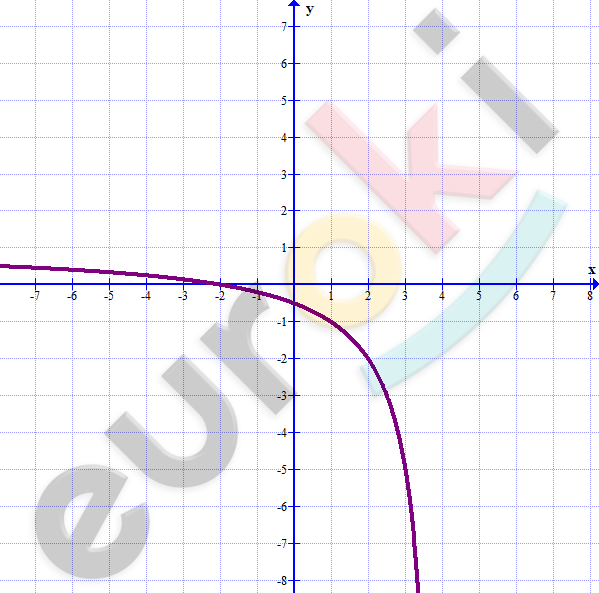
\[\frac{6}{x - 4} = y - 1\]

\[x - 4 = \frac{6}{y - 1}\]

\[x = \frac{6}{y - 1} + 4\]

\[y = \frac{6}{x - 1} + 4;\ \ y \in ( - \infty;4).\]

\[\textbf{д)}\ y = \frac{1}{1 + x^{2}};\ \ \ x \in \lbrack 0; + \infty)\]

\[1 + x^{2} = \frac{1}{y}\]

\[x^{2} = \frac{1}{y} - 1\]

\[x = \sqrt{\frac{1}{y} - 1}\]

\[y = \sqrt{\frac{1}{x} - 1\ };\ \ y \in \lbrack 0; + \infty).\]

\[\textbf{е)}\ y = \frac{1}{1 + x^{2}};\ \ x \in ( - \infty;0\rbrack\]

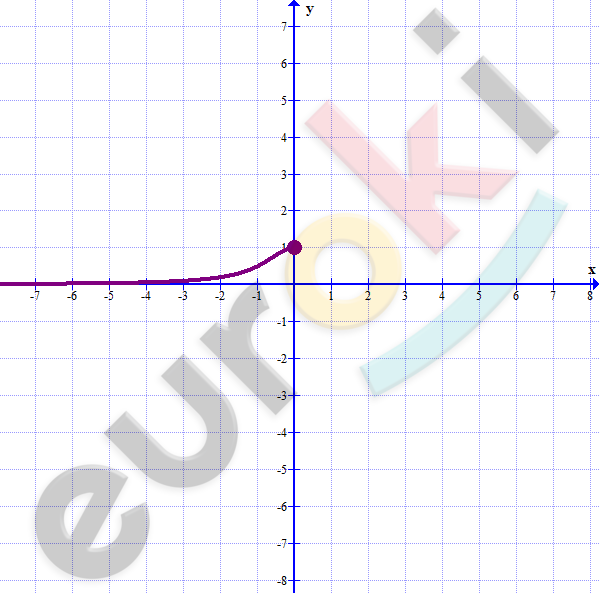
\[1 + x^{2} = \frac{1}{y}\]

\[x^{2} = \frac{1}{y} - 1\]

\[x = - \sqrt{\frac{1}{y} - 1}\]

\[y = - \sqrt{\frac{1}{x} - 1};y \in ( - \infty;0\rbrack\]