Решебник по алгебре 11 класс Никольский Параграф 9. Равносильность уравнений и неравенств системам Задание 50

\[\boxed{\mathbf{50.}}\]

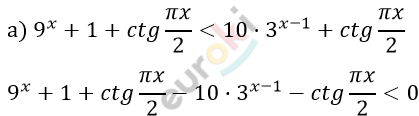
\[9^{x} - 10 \cdot 3^{x - 1} + 1 < 0\]

\[\left\{ \begin{matrix} 9^{x} - 10 \cdot 3^{x - 1} + 1 < 0 \\ \frac{\text{πx}}{2} \neq \pi n\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left( 3^{x} \right)^{2} - 10 \cdot \frac{3^{x}}{3} + 1 < 0\]

\[t = 3^{x}:\]

\[t^{2} - \frac{10}{3}t + 1 < 0\ \ \ | \cdot 3\]

\[3t^{2} - 10t + 3 < 0\]

\[D_{1} = 25 - 9 = 16\]

\[t_{1} = \frac{5 + 4}{3} = 3;\]

\[t_{2} = \frac{5 - 4}{3} = \frac{1}{3}.\]

\[\frac{1}{3} < t < 3\]

\[\frac{1}{3} < 3^{x} < 3\]

\[3^{- 1} < 3^{x} < 3^{1}\]

\[- 1 < x < 1.\]

\[\left\{ \begin{matrix} - 1 < x < 1 \\ x \neq 2n\ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} - 1 < x < 1 \\ x \neq 0\ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[Ответ:x \in ( - 1;0) \cup (0;1).\]

\[4^{x} - 9 \cdot 2^{x - 1} + 2 < 0\]

\[\left\{ \begin{matrix} 4^{x} - 9 \cdot 2^{x - 1} + 2 < 0 \\ \frac{\text{πx}}{2} \neq \frac{\pi}{2} + \pi n\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[\left( 2^{x} \right)^{2} - 9 \cdot \frac{2^{x}}{2} + 2 < 0\]

\[2^{x} = t:\]

\[t^{2} - \frac{9}{2}t + 2 < 0\ \ \ | \cdot 2\]

\[2t^{2} - 9t + 4 < 0\]

\[D = 81 - 32 = 49\]

\[t_{1} = \frac{9 + 7}{4} = 4;\]

\[t_{2} = \frac{9 - 7}{4} = \frac{1}{2};\]

\[\frac{1}{2} < t < 4\]

\[\frac{1}{2} < 2^{x} < 4\]

\[2^{- 1} < 2^{x} < 2^{2}\]

\[- 1 < x < 2.\]

\[\left\{ \begin{matrix} - 1 < x < 2 \\ x \neq 1 + 2n\ \\ \end{matrix} \right.\ \]

\[\left\{ \begin{matrix} - 1 < x < 2 \\ x \neq 1\ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[Ответ:x \in ( - 1;1) \cup (1;2).\]