Решебник по алгебре 11 класс Никольский Параграф 1. Функции и их графики Задание 48

\[\boxed{\mathbf{48.}}\]

\[\textbf{а)}\ y = x - \lbrack x\rbrack = \left\{ x \right\} - дробная\ \]

\[часть\ числа\ \text{x.}\]

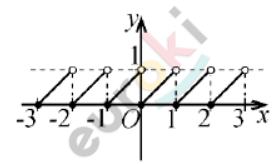
\[Функция\ возрастает\ на\ \]

\[промежутках\ \lbrack n;n + 1\rbrack;n \in Z.\]

\[\textbf{б)}\ y = \lbrack x\rbrack + x;\]

\[y = \lbrack x\rbrack - возрастает\ на\ R;\]

\[y = x - возрастает\ на\ R;\]

\[y = \lbrack x\rbrack + x - возрастает\ на\ \text{R.}\]

\[Функция\ возрастает\ на\ R.\]

\[\textbf{в)}\ y = |x - 4| + |x + 4|\]

\[|x - 4| + |x + 4| = 0\]

\[x - 4 = 0\ \ \ \ \ \ \ \ x + 4 = 0\]

\[x = 4\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = - 4\]

\[1)\ x \leq - 4:\]

\[y = - x + 4 - x - 4 = - 2x\]

\[Функция\ убывает,\ так\ как\ \]

\[k = - 2.\]

\[2) - 4 \leq x \leq 4:\]

\[y = - x + 4 + x + 4 = 8\]

\[Функция\ постоянна.\]

\[3)\ x \geq 4:\]

\[y = x - 4 + x + 4 = 2x\]

\[Функция\ возрастает,\ так\ \]

\[как\ k = 2.\]

\[Функция\ убывает\ на\]

\[\ промежутке\ ( - \infty;\ - 4\rbrack;\]

\[постоянна\ на\ промежутке\]

\[\ \lbrack - 4;4\rbrack;\]

\[возрастает\ на\ промежутке\ \]

\[\lbrack 4; + \infty).\]

\[\textbf{г)}\ y = |x - 8| + |x + 8|\]

\[|x - 8| + |x + 8| = 0\]

\[x = 8;\ \ \ \ x = - 8.\]

\[x \leq - 8:\]

\[y = - x + 8 - x - 8 = - 2x\]

\[функция\ убывает,\ так\ как\ k < 0.\]

\[- 8 \leq x \leq 8:\]

\[y = - x + 8 + x + 8 = 16\]

\[функция\ постоянна.\]

\[x \geq 8:\]

\[y = x - 8 + x + 8 = 2x\]

\[функция\ возрастает,\ так\]

\[\ как\ k > 0.\]

\[Функция\ убывает\ на\ \]

\[промежутке\ ( - \infty; - 8\rbrack;\]

\[постоянна\ на\ промежутке\ \]

\[\lbrack - 8;8\rbrack;\]

\[возрастает\ на\ промежутке\]

\[\ \lbrack 8; + \infty).\]

\[\textbf{д)}\ y = \sqrt{x^{2} + 2x + 1} +\]

\[+ \sqrt{x^{2} - 2x + 1} =\]

\[= \sqrt{(x + 1)^{2} + (x - 1)^{2}}\]

\[y = |x + 1| + |x - 1|\]

\[|x + 1| + |x - 1| = 0\]

\[x = - 1;\ \ \ x = 1.\]

\[x \leq - 1:\]

\[y = - x - 1 - x + 1 = - 2x\]

\[функция\ возрастает,\ так\ как\]

\[\ k < 0.\]

\[- 1 \leq x \leq 1:\]

\[y = - x + 1 + x + 1 = 2\]

\[функция\ постоянна.\]

\[x \geq 1:\]

\[y = x + 1 + x - 1 = 2x\]

\[функция\ возрастает,\ так\ как\]

\[\ k > 0.\]

\[Функция\ убывает\ на\]

\[\ промежутке\ ( - \infty; - 1\rbrack;\]

\[постоянна\ на\ промежутке\ \lbrack - 1;1\rbrack;\]

\[возрастает\ на\ промежутке\ \]

\[\lbrack 1; + \infty).\]

\[\textbf{е)}\ y = \sqrt{x^{2} + 6x + 9} +\]

\[+ \sqrt{x^{2} - 6x + 9} =\]

\[= \sqrt{(x + 3)^{2} + (x - 3)^{2}}\]

\[y = |x + 3| + |x - 3|\]

\[x = - 3;\ \ x = 3.\]

\[x \leq - 3:\]

\[y = - x - 3 - x + 3 = - 2x\]

\[функция\ убывает,\ так\ как\ k < 0.\]

\[- 3 \leq x \leq 3:\]

\[y = - x + 3 + x + 3 = 6\]

\[функция\ постоянна.\]

\[x \geq 3:\]

\[y = x + 3 + x - 3 = 2x\]

\[функция\ возрастает,\ так\ как\]

\[\ k > 0.\]

\[Функция\ убывает\ на\]

\[\ промежутке\ ( - \infty; - 3\rbrack;\]

\[постоянна\ на\ промежутке\]

\[\ \lbrack - 3;3\rbrack;\]

\[возрастает\ на\ промежутке\]

\[\ \lbrack 3; + \infty).\]