Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 818

\[a = x^{2} - x - 2;\ b = x + 3:\]

\[a^{2} + ab = 20b^{2}\]

\[a^{2} + ba - 20b^{2} = 0\]

\[D = b^{2} + 4 \bullet 20b^{2} =\]

\[= b^{2} + 80b^{2} = 81b^{2}\]

\[a_{1} = \frac{- b - 9b}{2} = - \frac{10b}{2} = - 5b;\]

\[a_{2} = \frac{- b + 9b}{2} = \frac{8b}{2} = 4b.\]

\[1)\ x^{2} - x - 2 = - 5(x + 3)\]

\[x^{2} - x - 2 = - 5x - 15\]

\[x^{2} + 4x + 13 = 0\]

\[D = 16 - 52 = - 36 < 0\]

\[x \in \varnothing.\]

\[2)\ x^{2} - x - 2 = 4(x + 3)\]

\[x^{2} - x - 2 = 4x + 12\]

\[x^{2} - 5x - 14 = 0\]

\[D = 25 + 56 = 81\]

\[x_{1} = \frac{5 - 9}{2} = - 2;\]

\[x_{2} = \frac{5 + 9}{2} = 7.\]

\[Ответ:\ - 2;\ 7.\ \]

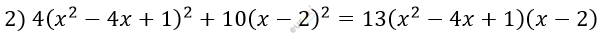
\[a = x^{2} - 4x + 1;\ b = x - 2:\]

\[4a^{2} + 10b^{2} = 13ab\]

\[4a^{2} - 13ba + 10b^{2} = 0\]

\[D = (13b)^{2} - 4 \bullet 4 \bullet 10b^{2} =\]

\[= 169b^{2} - 160b^{2} = 9b^{2}\]

\[a_{1} = \frac{13b - 3b}{2 \bullet 4} = \frac{10b}{8} = \frac{5b}{4};\]

\[a_{2} = \frac{13b + 3b}{2 \bullet 4} = \frac{16b}{8} = 2b.\]

\[1)\ x^{2} - 4x + 1 = \frac{5(x - 2)}{4}\]

\[4x^{2} - 16x + 4 = 5x - 10\]

\[4x^{2} - 21x + 14 = 0\]

\[D = 441 - 224 = 217\]

\[x = \frac{21 \pm \sqrt{217}}{2 \bullet 4} = \frac{21 \pm \sqrt{217}}{8}.\]

\[2)\ x^{2} - 4x + 1 = 2(x - 2)\]

\[x^{2} - 4x + 1 = 2x - 4\]

\[x^{2} - 6x + 5 = 0\]

\[D = 36 - 20 = 16\]

\[x_{1} = \frac{6 - 4}{2} = 1;\text{\ \ }\]

\[x_{2} = \frac{6 + 4}{2} = 5.\]

\[Ответ:\ \ 1;\ 5;\ \frac{21 \pm \sqrt{217}}{8}\text{.\ }\]