Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 819

\[1)\ \frac{x^{2} - x + 3}{x^{2} - x + 1} + \frac{x^{2} - x + 4}{x^{2} - x + 2} = 5\]

\[y = x^{2} - x:\]

\[\frac{y + 3}{y + 1} + \frac{y + 4}{y + 2} = 5\]

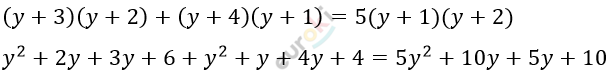
\[3y^{2} + 5y = 0\]

\[y(3y + 5) = 0\]

\[y_{1} = - \frac{5}{3};\text{\ \ \ }y_{2} = 0.\]

\[1)\ x^{2} - x = - \frac{5}{3}\]

\[3x^{2} - 3x + 5 = 0\]

\[D = 9 - 60 = - 51 < 0\]

\[x \in \varnothing.\]

\[2)\ x^{2} - x = 0\]

\[x(x - 1) = 0\]

\[x_{1} = 0;\text{\ \ \ }x_{2} = 1.\]

\[Ответ:\ \ 0;\ 1.\]

\[2)\ \frac{x^{2} + x + 2}{x^{2} + x + 1} + \frac{x^{2} + x + 6}{x^{2} + x + 3} = 4\]

\[y = x^{2} + x:\]

\[\frac{y + 2}{y + 1} + \frac{y + 6}{y + 3} = 4\]

\[2y^{2} + 4y = 0\]

\[2y(y + 2) = 0\]

\[y_{1} = - 2;\text{\ \ \ }y_{2} = 0.\]

\[1)\ x^{2} + x = - 2\]

\[x^{2} + x + 2 = 0\]

\[D = 1 - 8 = - 7 < 0\]

\[x \in \varnothing.\]

\[2)\ x^{2} + x = 0\]

\[x(x + 1) = 0\]

\[x_{1} = - 1;\text{\ \ \ }x_{2} = 0.\]

\[Ответ:\ - 1;\ 0.\]