Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 638

\[1)\sin\frac{\pi}{6} + i\sin\frac{\pi}{6} = \frac{1}{2} + \frac{1}{2}i =\]

\[= \frac{\sqrt{2}}{2}\left( \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i \right) =\]

\[= \frac{\sqrt{2}}{2}\left( \cos\frac{\pi}{4} + i\sin\frac{\pi}{4} \right).\]

\[2)\sin a + i\left( 1 - \cos a \right);0 < a < \frac{\pi}{2}:\]

\[r = \sqrt{\sin^{2}a + \left( 1 - \cos a \right)^{2}} =\]

\[= \sqrt{\sin^{2}a + 1 - 2\cos a + \cos^{2}a} =\]

\[= \sqrt{2 - 2\cos a} = \sqrt{4 \bullet \frac{1 - \cos a}{2}} =\]

\[= \sqrt{4\sin^{2}\frac{a}{2}} = 2\sin\frac{a}{2};\]

\[\cos\varphi = \frac{a}{r} = \frac{\sin a}{2\sin\frac{a}{2}} =\]

\[= \frac{2\sin\frac{a}{2} \bullet \cos\frac{a}{2}}{2\sin\frac{a}{2}} = \cos\frac{a}{2};\]

\[z = 2\sin\frac{a}{2}\left( \cos\frac{a}{2} + i\sin\frac{a}{2} \right).\]

\[3)\ (tg\ 1 - i)^{4}:\]

\[r = \sqrt{tg^{2}\ 1 + ( - 1)^{2}} =\]

\[= \sqrt{tg^{2}\ 1 + 1} = \sqrt{\frac{1}{\cos^{2}1}} = \frac{1}{\cos 1};\]

\[\cos\varphi = \frac{a}{r} = tg\ 1\ :\frac{1}{\cos 1} =\]

\[= \frac{\sin 1}{\cos 1} \bullet \cos 1 = \sin 1 =\]

\[= \cos\left( \frac{3\pi}{2} + 1 \right);\]

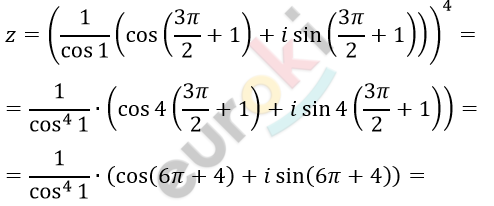
\[= \frac{1}{\cos^{4}1}\left( \cos 4 + i\sin 4 \right).\]

\[4)\ \frac{(1 + i)^{2n + 1}}{(1 - i)^{2n - 1}};\ \ \ n \in N:\]

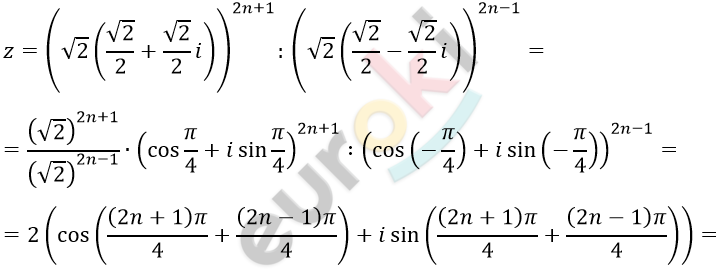
\[= 2\left( \cos\frac{4\pi n}{4} + i\sin\frac{4\pi n}{4} \right) =\]

\[2\left( \cos\text{πn} + i\sin\text{πn} \right);\]

\[z_{1} = 2\left( \cos 0 + i\sin 0 \right);\ \]

\[n - четное.\]

\[z_{2} = 2\left( \cos\pi + i\sin\pi \right);\]

\[\ n - нечетное.\]