Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 341

\[Квадрат\ касается\ стороны\ AB\ \]

\[в\ точке\ E.\]

\[1)\ Высота\ треугольника:\]

\[BD = BK + KD = x + a.\]

\[2)\ \mathrm{\Delta}\text{ABD}\sim\mathrm{\Delta}\text{EBK}:\]

\[\angle EBK = \angle ABD;\]

\[\angle BKE = \angle BDA.\]

\[3)\ Отсюда:\]

\[\frac{\text{AD}}{\text{EK}} = \frac{\text{BD}}{\text{BK}}\]

\[AD = \frac{EK \bullet BD}{\text{BK}} = \frac{\frac{a}{2} \bullet (x + a)}{x};\]

\[AC = 2AD = \frac{ax + a^{2}}{x}.\]

\[4)\ S(x) = \frac{1}{2}AC \bullet BD =\]

\[= \frac{1}{2} \bullet \frac{ax + a^{2}}{x} \bullet (x + a) =\]

\[= \frac{ax^{2} + a^{2}x + a^{2}x + a^{3}}{2x} =\]

\[= \frac{ax^{2} + 2a^{2}x + a^{3}}{2x};\]

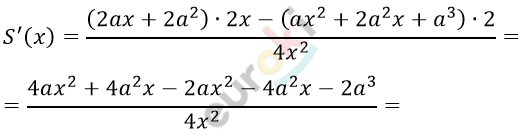
\[= \frac{2ax^{2} - 2a^{3}}{4x^{2}} = \frac{a\left( x^{2} - a^{2} \right)}{2x^{2}}.\]

\[5)\ Промежуток\ возрастания:\]

\[x^{2} - a^{2} \geq 0\]

\[(x + a)(x - a) \geq 0\]

\[x \leq - a;\ \ \ x \geq a.\]

\[6)\ Точка\ минимума:\]

\[x = a.\]

\[Ответ:\ \ x = a.\]