Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 1105

\[f(x) = - x^{3} + ax^{2} + bx + c;\]

\[1)\ Точки\ \text{A\ }и\ \text{B\ }лежат\ на\ \]

\[расстоянии\ \text{l\ }от\ x = 2:\]

\[A\left( 2 - l;\ f(2 - l) \right);\]

\[B\left( 2 + l;\ f(2 + l) \right).\]

\[2)\ f^{'}(x) =\]

\[= - \left( x^{3} \right)^{'} + a\left( x^{2} \right)^{'} + (bx + c)^{'} =\]

\[= - 3x^{2} + 2ax + b.\]

\[3)\ Касательные\ в\ точках\ \]

\[\text{A\ }и\ \text{B\ }параллельны:\]

\[- 3(2 - l)^{2} + 2a(2 - l) + b =\]

\[= - 3(2 + l)^{2} + 2a(2 + l) + b\]

\[- 3\left( 4 - 4l + l^{2} \right) + 4a - 2al =\]

\[= - 3\left( 4 + 4l + l^{2} \right) + 4a + 2al\]

\[- 12 + 12l - 3l^{2} - 2al =\]

\[= - 12 - 12l - 3l^{2} + 2al\]

\[12l + 12l - 2al - 2al = 0\]

\[24l - 4al = 0\]

\[6l - al = 0\]

\[6 - a = 0\]

\[a = 6.\]

\[4)\ Уравнение\ касательной\ \]

\[в\ точке\ t:\]

\[f^{'}(t) = - 3t^{2} + 12t + b;\]

\[f(t) = - t^{3} + 6t^{2} + bt + c;\]

\[5)\ В\ точке\ с\ x = 0:\]

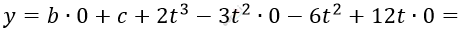
\[= c + 2t^{3} - 6t^{2}.\]

\[6)\ Касательная\ проходит\ \]

\[через\ точку\ (0;\ 2):\]

\[2 = c + 2(2 - l)^{3} - 6(2 - l)^{2}\]

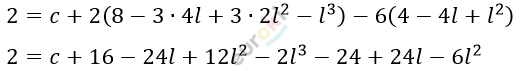
\[c - 2l^{3} + 6l^{2} - 10 = 0\]

\[c = 2l^{3} - 6l^{2} + 10.\]

\[7)\ Касательная\ проходит\ \]

\[через\ точку\ (0;\ 6):\]

\[6 = c + 2(2 + l)^{3} - 6(2 + l)^{2}\]

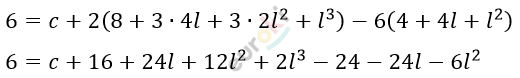
\[c + 2l^{3} + 6l^{2} - 14 = 0\]

\[c = - 2l^{3} - 6l^{2} + 14.\]

\[8)\ 2l^{3} - 6l^{2} + 10 = - 2l^{3} - 6l^{2} + 14\]

\[4l^{3} = 4\]

\[l^{3} = 1\]

\[l = 1;\]

\[c = 2 - 6 + 10 = 6.\]

\[9)\ Точка\ A:\]

\[2 - l = 2 - 1 = 1;\]

\[f(1) = - 1 + 6 + b + 6 = b + 11.\]

\[10)\ Точка\ B:\]

\[2 + l = 2 + 1 = 3;\]

\[f(3) = - 27 + 54 + 3b + 6 =\]

\[= 3b + 33.\]

\[11)\ Ординаты\ точек\ равны:\]

\[b + 11 = 3b + 33\]

\[- 2b = 22\]

\[b = - 11.\ \]

\[Ответ:\ \ a = 6;\ b = - 11;\ c = 6.\]