Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 1060

\[1)\ y = (x - 1)^{3} \bullet (x - 2)^{2}\]

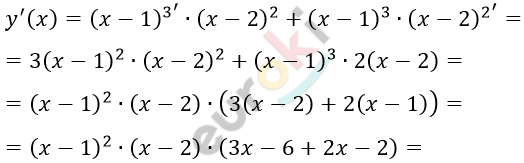
\[= (x - 1)^{2} \bullet (x - 2) \bullet (5x - 8).\]

\[Промежуток\ возрастания:\]

\[(5x - 8)(x - 2) \geq 0\]

\[x \leq 1,6;\ \ \ x \geq 2.\]

\[Ответ:\ \ \]

\[x = 1,6 - точка\ максимума;\]

\[x = 2 - точка\ минимума.\]

\[2)\ y = 4 + (6 - x)^{4}\]

\[y^{'}(x) = 0 + 4(6 - x)^{3} \bullet ( - 1) =\]

\[= - 4(6 - x)^{3}.\]

\[Промежуток\ возрастания:\]

\[(6 - x)^{3} \leq 0\]

\[6 - x \leq 0\]

\[x \geq 6.\]

\[Ответ:\ \ \]

\[x = 6 - точка\ минимума.\]