Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 1040

\[1)\ На\ отрезке\ \lbrack 0;\ 2\rbrack:\]

\[y = 4x^{2} - 4ax + a^{2} - 2a + 2\]

\[y^{'}(x) = 4 \bullet 2x - 4a \geq 0\]

\[8x \geq 4a\]

\[x \geq \frac{a}{2}.\]

\[Наименьшее\ значение:\]

\[y\left( \frac{a}{2} \right) =\]

\[= 4 \bullet \frac{a^{2}}{4} - 4a \bullet \frac{a}{2} + a^{2} - 2a + 2 =\]

\[= a^{2} - 2a^{2} + a^{2} - 2a + 2 =\]

\[= 2 - 2a;\]

\[2 - 2a = 3\]

\[2a = - 1\]

\[a = - \frac{1}{2};\]

\[x = - \frac{1}{2}\ :2 = - \frac{1}{4} < 0.\]

\[{Функция\ возрастает: }{y(0) = 4 \bullet 0^{2} - 4a \bullet 0 + a^{2} - 2a + 2 = 3;}\]

\[a^{2} - 2a - 1 = 0;\ \ \ \ \frac{a}{2} \leq 0;\]

\[D = 4 + 4 = 8\]

\[a = \frac{2 \pm 8}{2} = \frac{2 \pm 2\sqrt{2}}{2} =\]

\[= 1 \pm \sqrt{2};\ \ \ a \leq 0.\]

\[Функция\ убывает:\]

\[y(2) = 4 \bullet 2^{2} - 4a \bullet 2 + a^{2} - 2a + 2 = 3;\]

\[16 - 8a + a^{2} - 2a - 1 = 0;\ \ \frac{a}{2} \geq 2;\]

\[a^{2} - 10a + 15 = 0\]

\[D = 100 - 60 = 40\]

\[a = \frac{10 \pm \sqrt{40}}{2} = \frac{10 \pm 2\sqrt{10}}{2} =\]

\[= 5 \pm \sqrt{10};\ \ \ x \geq 2.\]

\[Ответ:\ \ 1 - \sqrt{2};\ 5 + \sqrt{10}.\]

\[2) > 1:\]

\[y = 4ax + \left| x^{2} - 8x + 7 \right|\]

\[x^{2} - 8x + 7 \geq 0\]

\[D = 8^{2} - 4 \bullet 7 = 64 - 28 = 36\]

\[x_{1} = \frac{8 - 6}{2} = 1;\]

\[x_{2} = \frac{8 + 6}{2} = 7;\]

\[(x - 1)(x - 7) \geq 0\]

\[x \leq 1;\ \ \ x \geq 7.\]

\[x \leq 1\ и\ x \geq 7:\]

\[y = 4ax + x^{2} - 8x + 7\]

\[y^{'}(x) = 4a + 2x - 8 \geq 0\]

\[2x \geq 8 - 4a\]

\[x \geq 4 - 2a.\]

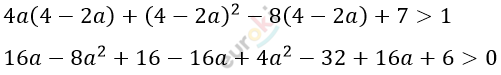
\[- 4a^{2} + 16a - 10 > 0\]

\[2a^{2} - 8a + 5 < 0\]

\[D = 64 - 40 = 24\]

\[a = \frac{8 \pm \sqrt{24}}{2 \bullet 2} = \frac{8 \pm 2\sqrt{6}}{4} =\]

\[= \frac{4 \pm \sqrt{6}}{2};\]

\[\frac{4 - \sqrt{6}}{2} < a < \frac{4 + \sqrt{6}}{2};\]

\[x = 4 - \left( 4 \pm \sqrt{6} \right) = \mp \sqrt{6}.\]

\[1 \leq x \leq 7:\]

\[y = 4ax - x^{2} + 8x - 7;\]

\[y^{'}(x) = 4a - 2x + 8 \geq 0;\]

\[2x \leq 8 + 4a\]

\[x \leq 4 + 2a\]

\[4a \bullet 1 - 1^{2} + 8 \bullet 1 - 7 > 1\]

\[4a - 1 + 8 - 8 > 0\]

\[4a > 1\]

\[a > \frac{1}{4}.\]

\[Ответ:\ \ a \in \left( \frac{1}{4};\ \frac{4 + \sqrt{6}}{2} \right).\]