Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 1027

\[1)\ y = 3^{x} + 1\]

\[D(x) = ( - \infty;\ + \infty);\]

\[ни\ четная,\ ни\ нечетная:\]

\[y( - x) = 3^{- x} + 1 = \frac{1}{3^{x}} + 1;\]

\[\lim_{x \rightarrow - \infty}\left( 3^{x} + 1 \right) = 0 + 1 = 1;\]

\[y^{'}(x) = \left( 3^{x} \right)^{'} + 1^{'} = 3^{x}\ln 3 > 0;\]

\[E(y) = (1;\ + \infty).\]

\[2)\ y = \left( \frac{1}{2} \right)^{x} - 3\]

\[D(x) = ( - \infty;\ + \infty);\]

\[ни\ четная,\ ни\ нечетная:\]

\[y( - x) = \left( \frac{1}{2} \right)^{- x} - 3 = 2^{x} - 3;\]

\[\lim_{x \rightarrow + \infty}\left( \left( \frac{1}{2} \right)^{x} - 3 \right) = 0 - 3 = - 3;\]

\[y^{'}(x) = {\left( \frac{1}{2} \right)^{x}}^{'} - 3^{'} =\]

\[= \left( \frac{1}{2} \right)^{x}\ln\left( \frac{1}{2} \right) < 0;\]

\[E(y) = ( - 3;\ + \infty);\]

\[3)\ y = \log_{2}(x + 1)\]

\[x + 1 > 0\]

\[x > - 1;\]

\[D(x) = ( - 1;\ + \infty);\]

\[ни\ четная,\ ни\ нечетная:\]

\[y( - x) = \log_{2}( - x + 1);\]

\[y^{'}(x) = \left( \log_{2}(x + 1) \right)^{'} =\]

\[= \frac{1}{(x + 1) \bullet \ln 2};\]

\[Промежуток\ возрастания:\]

\[x + 1 > 0.\]

\[x > - 1.\]

\[E(y) = ( - \infty;\ + \infty);\]

\[4)\ y = \log_{\frac{1}{3}}(x - 1)\]

\[x - 1 > 0\]

\[x > 1;\]

\[D(x) = (1;\ + \infty);\]

\[ни\ четная,\ ни\ нечетная:\]

\[y( - x) = \log_{\frac{1}{3}}( - x - 1);\]

\[y^{'}(x) = \left( \log_{\frac{1}{3}}(x - 1) \right)^{'} =\]

\[= \frac{1}{(x - 1) \bullet \ln\frac{1}{3}};\]

\[Промежуток\ убывания:\]

\[x - 1 > 0\]

\[x > 1.\]

\[E(y) = ( - \infty;\ + \infty).\]

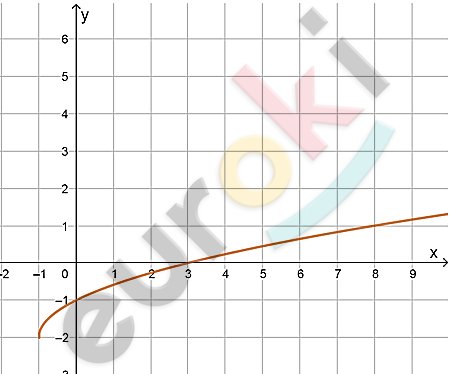
\[5)\ y = \sqrt{x + 1} - 2\]

\[x + 1 \geq 0\]

\[x \geq - 1;\]

\[D(x) = \lbrack - 1;\ + \infty);\]

\[ни\ четная,\ ни\ нечетная:\]

\[y( - x) = \sqrt{- x + 1} - 2;\]

\[y^{'}(x) = \frac{(x + 1)^{'}}{2\sqrt{x + 1}} - 2^{'} =\]

\[= \frac{1}{2\sqrt{x + 1}} > 0;\]

\[y( - 1) = \sqrt{- 1 + 1} - 2 = - 2;\]

\[E(y) = \lbrack - 2;\ + \infty).\]

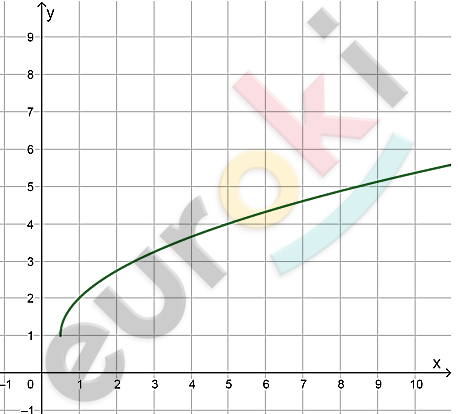
\[6)\ y = \sqrt{2x - 1} + 1\]

\[2x - 1 \geq 0\]

\[x \geq 0,5;\]

\[D(x) = \lbrack 0,5;\ + \infty);\]

\[ни\ четная,\ ни\ нечетная:\]

\[y( - x) = \sqrt{- 2x - 1} + 1;\]

\[y^{'}(x) = \frac{(2x - 1)^{'}}{2\sqrt{2x - 1}} - 1^{'} =\]

\[= \frac{2}{2\sqrt{2x - 1}} > 0;\]

\[y(0,5) = \sqrt{2 \bullet 0,5 - 1} + 1 = 1;\]

\[E(y) = \lbrack 1;\ + \infty).\]