Решебник по алгебре и начала математического анализа 11 класс Колягин Задание 10

\[1)\ y = \frac{\cos x}{1,5 - \sin x}\]

\[- 1 \leq - \sin x \leq 1;\]

\[0,5 \leq 1,5 - \sin x \leq 2,5;\]

\[\frac{2}{5} \leq \frac{1}{1,5 - \sin x} \leq 2;\]

\[- 2 \leq \frac{\cos x}{1,5 - \sin x} \leq 2.\]

\[Что\ и\ требовалось\ доказать.\]

\[2)\ y = \frac{1}{\sqrt{3} - \left( \sin x + \cos x \right)}\]

\[- 1 \leq \sin\left( x + \frac{\pi}{4} \right) \leq 1;\]

\[- 1 \leq \cos\frac{\pi}{4}\sin x + \sin\frac{\pi}{4}\cos x \leq 1;\]

\[- 1 \leq \frac{\sqrt{2}}{2}\left( \sin x + \cos x \right) \leq 1;\]

\[- \sqrt{2} \leq \sin x + \cos x \leq \sqrt{2};\]

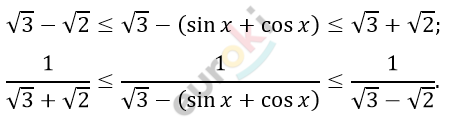
\[Что\ и\ требовалось\ доказать.\]