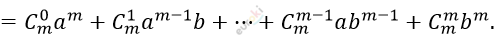Решебник по алгебре и начала математического анализа 11 класс Колягин Вопросы к главе V

\[\mathbf{1.}\]

\[\mathbf{\ }Комбинаторика\ занимается\ \]

\[решением\ задач,связанных\]

\[с\ выбором\ и\ расположением\ \]

\[элементов\ множества\ в\ \]

\[соответствии\ с\ заданными\ \]

\[правилами.\]

\[\mathbf{2.}\ \]

\[Если\ существует\ n\ вариантов\ \]

\[выбора\ первого\ элемента\ и\ для\]

\[каждого\ из\ них\ имеется\ \text{m\ }\]

\[вариантов\ выбора\ второго\ \]

\[элемента,\ то\ существует\ n \bullet m\ \]

\[различных\ пар\ с\ выбранными\ \]

\[первым\ и\ вторым\ элементами.\]

\[\mathbf{3.\ }\]

\[Соединения,\ содержащие\ \text{n\ }\]

\[элементов,\ выбираемых\ из\ \]

\[элементов\ \text{m\ }различных\ видов,\ \]

\[и\ отличающиеся\ одно\ от\ \]

\[другого\ составом\ или\ порядком\ \]

\[следования\ элементов,\ \]

\[называют\ размещениями\ с\ \]

\[повторениями\ из\ \text{m\ }по\ n:\]

\[{\overline{A}}_{m}^{n} = m^{n}.\]

\[\mathbf{4.\ }\]

\[Перестановками\ из\ \text{n\ }различных\ \]

\[элементов\ называются\]

\[соединения,\ которые\ состоят\ из\ \]

\[имеющихся\ \text{n\ }элементов\ и\ \]

\[отличаются\ только\ порядком\ \]

\[их\ расположения:\]

\[P_{n} = n!.\]

\[\mathbf{5.\ }\]

\[Размещениями\ из\ \text{m\ }элементов\ \]

\[по\ \text{n\ }элементов\ (n \leq m)\]

\[называются\ такие\ соединения,\ \]

\[каждое\ из\ которых\ содержит\ \]

\[\text{n\ }элементов,\ взятых\ из\ данных\ \]

\[\text{m\ }разных\ элементов,\ и\ которые\ \]

\[отличаются\ одно\ от\ другого\ \]

\[либо\ самими\ элементами,\ либо\ \]

\[порядком\ их\ расположения:\]

\[A_{m}^{n} = \frac{m!}{(m - n)!}.\]

\[\mathbf{6.}\ \]

\[Сочетаниями\ из\ \text{m\ }элементов\ \]

\[по\ \text{n\ }в\ каждом\ (n \leq m)\]

\[называются\ такие\ соединения,\ \ \]

\[каждое\ из\ которых\ содержит\ n\ \]

\[элементов,\ взятых\ из\ данных\ \text{m\ }\]

\[различных\ элементов,\ и\ которые\ \]

\[отличаются\ одно\ от\ другого\ по\]

\[крайней\ мере\ одним\ элементом:\]

\[C_{m}^{n} = \frac{A_{m}^{n}}{P_{n}} = \frac{m!}{(m - n)!n!}.\]

\[\mathbf{7.\ }\]

\[\mathbf{Свойства\ сочетаний\ без\ }\]

\[\mathbf{повторений}\mathbf{:}\]

\[C_{m}^{n} = C_{m}^{m - n};\text{\ \ \ }\]

\[C_{m}^{n} + C_{m}^{n + 1} = C_{m + 1}^{n + 1}.\]

\[\mathbf{8.}\mathbf{\ }\]

\[\mathbf{Треугольником\ Паскаля\ }\]

\[\mathbf{называют\ бесконечную}\]

\[\mathbf{таблицу\ биноминальных\ }\]

\[\mathbf{коэффициентов,\ имеющую}\]

\[\mathbf{треугольную\ форму,\ на\ }\]

\[\mathbf{вершине\ и\ по\ бокам\ стоят}\]

\[\mathbf{единицы,\ каждое\ число\ равно\ }\]

\[\mathbf{сумме\ двух\ чисел,\ }\]

\[\mathbf{расположенных\ над\ ним}\mathbf{.}\]

\[\mathbf{9.\ }\]

\[\mathbf{Формула\ бинома\ Ньютона}\mathbf{:}\]

\[(a + b)^{m} =\]