Решебник по алгебре и начала математического анализа 11 класс Колягин Вопросы к главе IV

\[\mathbf{1.}\]

\[\mathbf{\ }Функция\ F(x)\ называется\ \]

\[первообразной\ для\ \ функции\ \]

\[f(x)\ на\ некотором\ интервале,\ \ \]

\[если\ для\ всех\ \text{x\ }из\ интервала\ \]

\[выполняется\ равенство:\]

\[F^{'}(x) = f(x).\]

\[\mathbf{2.}\ \]

\[Если\ F(x) - первообразная\ для\ \]

\[функции\ f(x)\ на\ \ некотором\ \]

\[промежутке,\ то\ и\ функция\ \ \]

\[F(x) + C,\ где\ C - любая\ \]

\[постоянная,\ является\ \ \]

\[первообразной\ для\ функции\ \]

\[f(x)\ на\ этом\ промежутке.\]

\[\mathbf{3}\mathbf{.}\]

\[y = x^{p}\ (p \neq - 1)\]

\[F(x) = \frac{x^{p + 1}}{p + 1} + C;\]

\[y = \frac{1}{x}\ (x > 0,\ x < 0)\]

\[F(x) = \ln|x| + C;\]

\[y = e^{x}\]

\[F(x) = e^{x} + C;\]

\[y = \sin x\]

\[F(x) = - \cos x + C;\]

\[y = \cos x\]

\[F(x) = \sin x + C.\]

\[\mathbf{4.}\ \]

\[Пусть\ F(x)\ и\ G(x) -\]

\[первообразные\ соответственно\ \]

\[для\ функций\ f(x)\ и\ g(x)\ на\ \]

\[некотором\ промежутке,то\ есть\ \]

\[F^{'}(x) = f(x);\ \ \]

\[G^{'}(x) = g(x);\ \]

\[a,\ b,\ k - постоянные;\text{\ k} \neq 0:\]

\[1)\ F(x) + G(x) = первообразная\ \]

\[для\ функции\ f(x) + g(x);\]

\[2)\ aF(x) - первообразная\ для\ \]

\[функции\ \text{af}(x);\]

\[3)\ \frac{1}{k}F(kx + b) - первообразная\ \]

\[для\ функции\ f(kx + b).\]

\[\mathbf{5.}\ \]

\[y = e^{x - 2};\text{\ \ \ y} = 0;\text{\ \ \ }\]

\[x = 1;\ \ \ x = 4;\]

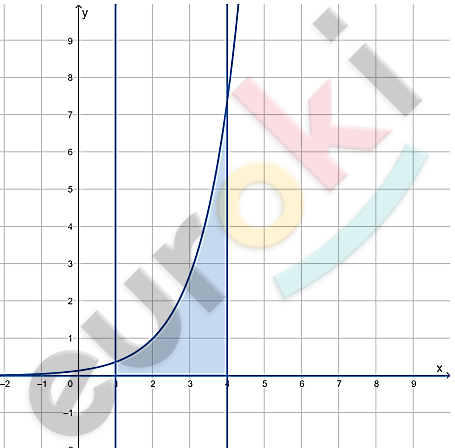
\[\mathbf{6.}\ \]

\[Криволинейной\ трапецией\ \]

\[назвают\ фигуру,\ ограниченную\ \]

\[отрезками\ прямых\ x = a;\ x = b;\text{\ \ }\]

\[y = 0\ и\ графиком\ непрерывной\ \]

\[функции\ y = f(x),\ такой,\ что\]

\[f(x) \geq 0\ на\ отрезке\ \lbrack a;\ b\rbrack\ и\ \]

\[f(x) > 0\ при\ x \in (a;\ b).\]

\[\mathbf{7.\ }\]

\[\mathbf{Формула\ Ньютона}\text{-}\mathbf{Лейбница}\mathbf{:}\]

\[S = \int_{a}^{b}{f(x)\text{dx}} = F(b) - F(a).\]

\[\mathbf{8.\ }\]

\[f(x) = x^{2} - 4;\text{\ \ \ y} = 0;\text{\ \ \ }\]

\[x = a;\ \ \ x = b;\]

\[- 2 < a < b < 2;\text{\ \ \ }\]

\[S = \int_{a}^{b}{\left( - f(x) \right)\text{dx}}.\]

\[\mathbf{9.}\]

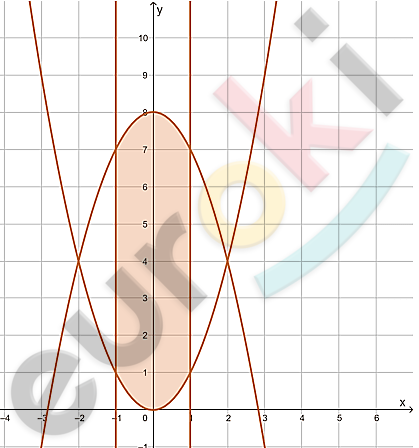
\[f_{1}(x) = x^{2};\text{\ \ \ }f_{2}(x) = 8 - x^{2};\text{\ \ \ }\]

\[x = a;\ \ \ x = b;\]

\[- 2 < a < b < 2;\text{\ \ \ }\]

\[S = \int_{a}^{b}{\left( f_{2}(x) - f_{1}(x) \right)\text{dx}}.\]

\[\mathbf{10.}\ \]

\[Вычисление\ пути\ и\ работы:\]

\[s = \int_{a}^{b}{v(t)\text{dt}};\]

\[A = \int_{a}^{b}{F(x)\text{dx}}.\]

\[\mathbf{11.\ }\]

\[Интегральной\ суммой\ функции\ \ \]

\[y = f(x)\ на\ отрезке\ \lbrack a;\ b\rbrack\ \]

\[называют\ сумму\ произведений\ \]

\[длин\ отрезков\ \mathrm{\Delta}x_{n}\ на\ значения\]

\[функции\ f\left( c_{n} \right)\ в\ точках\ из\ этих\ \]

\[отрезков:\]

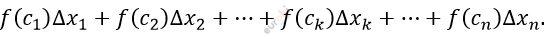
\[\mathbf{12.\ }\]

\[Определенным\ интегралом\ от\ \]

\[функции\ y = f(x)\ на\ отрезке\ \]

\[\lbrack a;\ b\rbrack\ называют\ интегральную\ \ \]

\[сумму\ данной\ функции\ на\ этом\ \]

\[отрезке,\ длина\ наибольшего\]

\[отрезка\ \mathrm{\Delta}x_{n}\ которой\ стремится\ \]

\[к\ нулю,\ и\ обозначают:\]

\[\int_{a}^{b}{f(x)\text{dx}}.\]

\[\mathbf{13.\ }\]

\[\mathbf{Уравнением\ гармонического\ }\]

\[\mathbf{колебания\ }называют\ \]

\[дифференциальное\ уравнение:\]

\[y^{''} + \omega^{2}y = 0.\]

\[Его\ решениями\ являются\ \]

\[функции:\]

\[\cos\text{ωx};\text{\ \ \ }\sin\text{ωx};\]

\[y = C_{1}\cos\text{ωx} + C_{2}\sin\text{ωx}.\]