Решебник по алгебре и начала математического анализа 11 класс Колягин Вопросы к главе II

\[\mathbf{1.\ }\]

\[Словесный\ \]

\[(описанием\ закономерности);\]

\[аналитический\ \]

\[\left( формулой\text{\ n}\text{-}го\ члена \right);\]

\[рекуррентный\ \]

\[(через\ предыдущие\ члены).\]

\[\mathbf{2.}\ \]

\[Сходящейся\ называется\ \]

\[последовательность,\]

\[для\ которой\ существует\ \]

\[предел\ при\ n \rightarrow + \infty.\]

\[\mathbf{3.\ }\]

\[\mathbf{Монотонными\ называют\ }\]

\[\mathbf{все\ возрастающие,}\mathbf{\ }\]

\[\mathbf{неубывающие,\ убывающие\ }\]

\[\mathbf{и\ невозрастающие\ }\]

\[\mathbf{последовательности}\mathbf{.}\]

\[\mathbf{4.}\ \]

\[Асимптоты:\]

\[y = \frac{1}{(x + 1)^{2}} + 2;\]

\[x = - 1 - вертикальная;\]

\[y = 2 - горизонтальная.\]

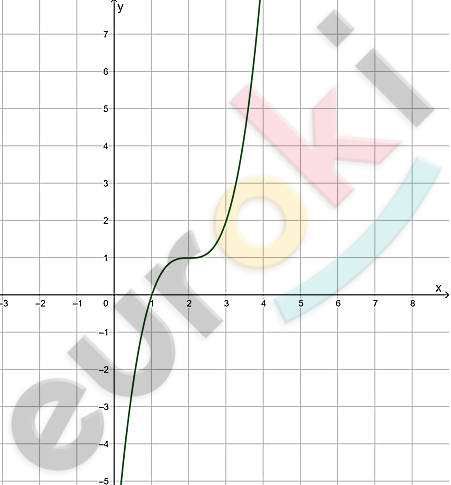
\[\mathbf{5.\ }\]

\[Непрерывная\ функция:\]

\[y = (x - 2)^{3} + 1.\]

\[\mathbf{6.}\ \]

\[Мгновенной\ скоростью\ \]

\[(скоростью\ точки\ в\ момент\ t)\]

\[называют\ предел,\ к\ которому\ \ \]

\[стремится\ средняя\ скорость,\ \]

\[когда\ h \rightarrow 0,\ то\ есть\ скорость\ \ \]

\[v(t)\ в\ момент\ t\ определяется\ \]

\[равенством:\]

\[v(t) = \lim_{h \rightarrow 0}\frac{s(t + h) - s(t)}{h}.\]

\[\mathbf{7.\ }\]

\[Производной\ функции\ f(x)\ в\ \]

\[точке\ x_{0}\ называется\ предел\]

\[разностного\ отношения\ при\ h \rightarrow 0:\]

\[f^{'}\left( x_{0} \right) = \lim_{h \rightarrow 0}\frac{f\left( x_{0} + h \right) - f\left( x_{0} \right)}{h}.\]

\[\mathbf{8.\ }\]

\[Мгновенную\ скорость\ v(t)\]

\[называют\ производной\ \]

\[функции\ s(t):\]

\[v(t) = s^{'}(t).\]

\[\mathbf{9.\ }\]

\[1)\ производная\ суммы\ равна\ \]

\[сумме\ производных:\]

\[\left( f(x) + g(x) \right)^{'} = f^{'}(x) + g^{'}(x);\]

\[2)\ функции\ f(x)\ и\ g(x)\ \]

\[дифференцируемы\ в\ точке\ x,\]

\[тогда\ в\ этой\ точке\ функция\ \]

\[f(x) \bullet g(x)\ имеет\ производную,\ \]

\[которая\ выражается\ формулой:\]

\[\left( f(x) \bullet g(x) \right)^{'} =\]

\[= f^{'}(x) \bullet g(x) + f(x) \bullet g^{'}(x);\]

\[3)\ функции\ f(x)\ и\ g(x)\ \ \]

\[дифференцируемы\ в\ точке\ \]

\[\text{x\ }и\ g(x) \neq 0,\ тогда\ в\ точке\ \text{x\ \ }\]

\[функция\ \frac{f(x)}{g(x)}\ имеет\ \]

\[производную,\ которая\ \]

\[выражается\ формулой:\]

\[\left( \frac{f(x)}{g(x)} \right)^{'} =\]

\[= \frac{f^{'}(x) \bullet g(x) - f(x) \bullet g^{'}(x)}{g^{2}(x)}.\]

\[\mathbf{10.\ }\]

\[y = x^{p}\ (p \in R)\]

\[y^{'}(x) = px^{p - 1}.\]

\[y = \sin x\]

\[y^{'}(x) = \cos x.\]

\[y = \cos x\]

\[y^{'}(x) = - \sin x.\]

\[y = e^{x}\]

\[y^{'}(x) = e^{x}.\]

\[\mathbf{11.}\mathbf{\ }\]

\[\mathbf{Угловым\ коэффициентом\ }\]

\[\mathbf{прямой\ называют}\mathbf{\ тангенс}\]

\[\mathbf{угла\ наклона\ этой\ прямой\ }\]

\[\mathbf{к\ оси\ абсцисс}\mathbf{:}\]

\[k = tg\ a.\]

\[\mathbf{12.\ }Уравнение\ прямой,\ угловой\ \]

\[коэффициент\ которой\ k,\]

\[проходящей\ через\ \]

\[точку\ \left( x_{0};\ y_{0} \right):\]

\[y = k\left( x - x_{0} \right) + y_{0}.\]

\[\mathbf{13.\ }\]

\[Геометрический\ смысл\ \]

\[производной\ состоит\ в\ том,\]

\[что\ значение\ производной\ \]

\[f(x)\ в\ точке\ x_{0}\ равно\ угловому\ \]

\[коэффициенту\ касательной\ к\]

\[графику\ функции\ y = f(x)\ в\ \]

\[точке\ \left( x_{0};\ f\left( x_{0} \right) \right).\]

\[\mathbf{14.\ }\]

\[Число\ \text{a\ }называют\ пределом\ \]

\[последовательности\ \left\{ x_{n} \right\},если\ \]

\[для\ каждого\ \varepsilon > 0\ существует\ \]

\[такой\ номер\ N_{\varepsilon},\ что\ для\ всех\ \]

\[\ n \geq N_{\varepsilon}\ выполняется\ \]

\[неравенство\ \left| x_{n} - a \right| < \varepsilon,\ \]

\[если\ a - предел\ \]

\[последовательности:\ \]

\[\lim_{n \rightarrow \infty}x_{n} = a;\]

\[x_{n} \rightarrow a\ при\ n \rightarrow \infty.\]

\[\mathbf{15.\ }\]

\[Число\ \text{A\ }называется\ пределом\ \]

\[функции\ f(x)\ в\ точке\ a\]

\[(при\ x,\ стремящемся\ к\ a),\ если\ \]

\[для\ любого\ \varepsilon > 0\ найдется\]

\[число\ \delta > 0,\ такое,\ что\ для\ x,\]

\[\ удовлетворяющих\ условию\ \]

\[0 < |x - a| < \delta,\ выполняется\ \]

\[неравенство\ \left| f(x) - A \right| < \varepsilon.\]

\[\mathbf{16.\ }\]

\[Функция\ f(x)\ называется\ \ \]

\[непрерывной\ в\ некоторой\ \]

\[точке\ a,\ если\ \lim_{x \rightarrow a}{f(x)} = f(a).\]

\[\mathbf{17.\ }\]

\[Пусть\ функция\ g(x)\ имеет\ \]

\[производную\ в\ точке\ x,\ а\]

\[функция\ f(t)\ имеет\ \]

\[производную\ в\ точке\ t = g(x),\ \]

\[тогда\ сложная\ функция\ f\left( g(x) \right)\ \]

\[имеет\ производную\ в\ точке\ x,\]

\[которая\ выражается\ формулой:\]

\[\left( f\left( g(x) \right) \right)^{'} = f^{'}\left( g(x) \right) \bullet g^{'}(x).\]

\[Пусть\ y = f(x)\ и\ x = \varphi(y)\ \]

\[взаимно\ обратные\ \ функции,\ \]

\[дифференцируемые\ в\ точке\ x:\]

\[\varphi^{'}(x) = \frac{1}{f^{'}\left( \varphi(x) \right)}.\]

\[\mathbf{18.\ }\]

\[\left( \text{tg\ x} \right)^{'} = \left( \frac{\sin x}{\cos x} \right)^{'} =\]

\[= \frac{\cos x \bullet \cos x - \sin x \bullet \left( - \sin x \right)}{\cos^{2}x} =\]

\[= \frac{\cos^{2}x + \sin^{2}x}{\cos^{2}x} = \frac{1}{\cos^{2}x};\]

\[\left( \text{ctg\ x} \right)^{'} = \left( \frac{\cos x}{\sin x} \right)^{'} =\]

\[= \frac{- \sin x \bullet \sin x - \cos x \bullet \cos x}{\sin^{2}x} =\]

\[= - \frac{\sin^{2}x + \cos^{2}x}{\sin^{2}x} = - \frac{1}{\sin^{2}x}.\]

\[\mathbf{19.}\ \]

\[Касательной\ функции\ в\ точке\ x_{0}\ \]

\[называют\ такую\ прямую,\ угловой\ \]

\[коэффициент\ которой\ равен\ \]

\[производной\ функции\ f(x)\ в\ \]

\[этой\ точке,\ проходящую\ через\ \]

\[точку\ \left( x_{0};\ f\left( x_{0} \right) \right):\]

\[y = f\left( x_{0} \right) + f^{'}\left( x_{0} \right)\left( x - x_{0} \right).\]

\[\mathbf{20.\ }\]

\[Число\ A_{1}\ называется\ пределом\ \]

\[слева\ функции\ f(x)\ в\ точке\ a,\]

\[если\ для\ любого\ \varepsilon > 0\ \ \]

\[существует\ число\ \delta > 0,\ такое,\ \]

\[что\ для\ всех\ x,\ удовлетворяющих\ \]

\[\ условию\ a - \delta < x < a,\ \]

\[выполняется\ неравенство\ \]

\[\left| f(x) - A_{1} \right| < \varepsilon:\]

\[\lim_{\begin{matrix} x \rightarrow a \\ x < a \\ \end{matrix}}{f(x)} = A_{1};\text{\ \ \ }\]

\[\lim_{x \rightarrow a - 0}{f(x)} = A_{1}.\]

\[Число\ A_{2}\ называется\ пределом\ \]

\[справа\ функции\ f(x)\ в\ точке\ a,\]

\[если\ для\ любого\ \varepsilon > 0\ \ \]

\[существует\ число\ \delta > 0,\ такое,\ \]

\[что\ для\ всех\ x,\ \]

\[удовлетворяющих\ условию\ \]

\[a < x < a + \delta,\ выполняется\ \]

\[неравенство\ \left| f(x) - A_{2} \right| < \varepsilon:\]

\[\lim_{\begin{matrix} x \rightarrow a \\ x > a \\ \end{matrix}}{f(x)} = A_{2};\text{\ \ \ }\]

\[\lim_{x \rightarrow a + 0}{f(x)} = A_{2}.\]

\[\mathbf{21.\ }\]

\[Функцию\ \alpha(x)\ называют\ \]

\[бесконечно\ малой\ при\ x \rightarrow a,\]

\[если\ выполняется\ равенство\]

\[\lim_{x \rightarrow a}{\alpha(x)} = 0.\]

\[\mathbf{22.\ }\]

\[1)\lim_{x \rightarrow a}{f(x)} = a;\ \ \lim_{x \rightarrow a}{g(x)} = B:\]

\[\lim_{x \rightarrow a}\left( f(x) + g(x) \right) = A + B;\]

\[\lim_{x \rightarrow a}\left( f(x)g(x) \right) = AB;\]

\[\lim_{x \rightarrow a}\frac{f(x)}{g(x)} = \frac{A}{B}\ при\ B \neq 0.\]

\[2)\ Если\ в\ некоторой\ проколотой\ \]

\[окрестности\ точки\ a\ справедливы\]

\[неравенства\ f(x) \leq \varphi(x) \leq g(x)\]

\[и\ \lim_{x \rightarrow a}{f(x)} = A,\ \lim_{x \rightarrow a}{g(x)} = A,\ \]

\[то\ \lim_{x \rightarrow a}{\varphi(x)}\ есть\ и\ равен\ A.\]

\[\mathbf{23.\ }\]

\[1)\ Если\ функция\ f(x)\ \]

\[непрерывна\ на\ отрезке\ \lbrack a;\ b\rbrack,\ \]

\[то\ она\ принимает\ на\ этом\ \]

\[отрезке\ свое\ наибольшее\ и\ \]

\[свое\ наименьшее\ значения,\ то\ \]

\[есть\ существуют\ точки\ \]

\[x_{1} \in \lbrack a;\ b\rbrack,\ x_{2} \in \lbrack a;\ b\rbrack;\]

\[такие,\ что\ для\ всех\ x \in \lbrack a;\ b\rbrack\ \]

\[выполняются\ неравенства:\]

\[f(x) \geq f\left( x_{1} \right),\ f(x) \leq f\left( x_{2} \right).\]

\[2)\ Если\ функция\ f(x)\ \]

\[непрерывна\ на\ отрезке\ \lbrack a;\ b\rbrack\ и\ \]

\[f(a) \neq f(b),\ то\ она\ принимает\ \]

\[на\ этом\ отрезке\ любое\]

\[значение\ C,\ заключенной\ \]

\[между\ f(a)\ и\ f(b),\ то\ есть\ \]

\[сущестует\ точка\ x_{0},\ такая,\ \]

\[что\ a < x_{0} < b\ и\ f\left( x_{0} \right) = C.\]

\[3)\ Если\ функция\ f(x)\ \]

\[непрерывна\ и\ возрастает\ на\ \]

\[отрезке\ \lbrack a;\ b\rbrack,\ то\ на\ отрезке\]

\[\left\lbrack f(a);\ f(b) \right\rbrack\ определена\ \]

\[обратная\ к\ f(x)\ функция,\ \]

\[которая\ является\ непрерывной\ \]

\[и\ возрастающей.\]

\[\mathbf{24.\ }\]

\[y = \arcsin x\]

\[y^{'}(x) = \frac{1}{\sqrt{1 - x^{2}}};\text{\ \ }|x| < 1.\]

\[y = arctg\ x\]

\[y^{'}(x) = \frac{1}{1 + x^{2}};\ \ \ x \in R.\]

\[\mathbf{25.\ }\]

\[Пусть\ функция\ f(x)\ имеет\ \]

\[производную\ в\ точке\ x_{0},\ а\ \]

\[\mathrm{\Delta}f = f\left( x_{0} + \mathrm{\Delta}x \right) - f\left( x_{0} \right)\ \]

\[является\ приращением\ функции\ \ \]

\[f(x)\ в\ точке\ x_{0},\ соответствующее\ \]

\[приращению\ аргумента\ \mathrm{\Delta}x:\]

\[\mathrm{\Delta}f = f^{'}\left( x_{0} \right)\mathrm{\Delta}x + \alpha(\mathrm{\Delta}x) \bullet \mathrm{\Delta}x;\]

\[\alpha(\mathrm{\Delta}x) \rightarrow 0\ при\ \mathrm{\Delta}x \rightarrow 0.\]

\[Первое\ слагаемое\ в\ формуле,\ \]

\[то\ есть\ f^{'}\left( x_{0} \right)\mathrm{\Delta}x,\ называется\]

\[дифференциалом\ функции\ \]

\[f(x)\ в\ точке\ x_{0}\ и\ обозначается\]

\[\text{df}\left( x_{0} \right):\]

\[\ \text{df}\left( x_{0} \right) = f^{'}\left( x_{0} \right)\mathrm{\Delta}x.\]

\[\mathbf{26.\ }\]

\[\mathbf{Е}сли\ функция\ f(x)\ имеет\ \]

\[производную\ в\ точке\ x_{0},\]

\[то\ дифференциал\ этой\ \]

\[функции\ при\ x = x_{0}\ равен\ \]

\[приращению\ ординаты\ \]

\[касательной\ в\ точке\ \left( x_{0};\ f\left( x_{0} \right) \right)\ \]

\[при\ изменении\ аргумента\ от\ \]

\[x_{0}\ до\ x_{0} + h = x_{0} + \mathrm{\Delta}x.\]

\[Пусть\ s\left( t_{0} \right) - координата\ \]

\[движущейся\ точки\ в\ момент\]

\[времени\ t_{0},\ тогда\ дифференциал\ \]

\[\text{ds}\left( t_{0} \right)\ равен\ приращению\]

\[s\left( t_{0} + \mathrm{\Delta}t \right) - s\left( t_{0} \right)\ функции\ s(t)\ \]

\[за\ промежуток\ времени\ от\ t_{0}\ \]

\[до\ t_{0} + \mathrm{\Delta}t,\ если\ в\ течение\ этого\ \]

\[промежутка\ материальная\ \]

\[точка\ движется\ со\ скоростью\ \]

\[v\left( t_{0} \right) = s^{'}\left( t_{0} \right).\]