Решебник по алгебре и начала математического анализа 11 класс Колягин Проверь себя III. Сложный вариант

\[\mathbf{1}.\]

\[y = x^{3} + 3ax;\]

\[y^{'}(x) = 3x^{2} + 3a \geq 0;\]

\[3\left( x^{2} + a \right) \geq 0\]

\[a \geq 0.\]

\[Ответ:\ \ \lbrack 0;\ + \infty).\]

\[\mathbf{2}\text{.\ }\]

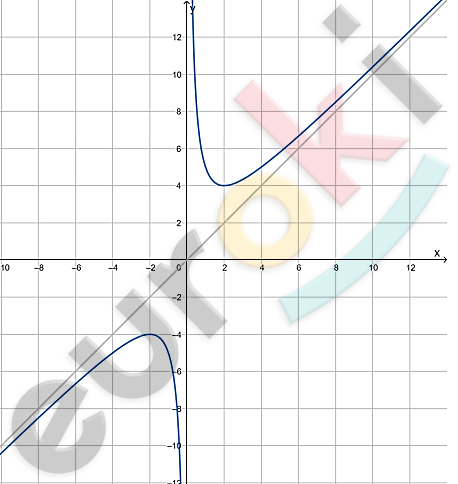
\[y = x + \frac{4}{x};\]

\[y^{'}(x) = 1 - \frac{4}{x^{2}} \geq 0;\]

\[\frac{x^{2} - 4}{x^{2}} \geq 0\]

\[\frac{(x + 2)(x - 2)}{x^{2}} \geq 0\]

\[x \leq - 2;\ \ \ x \geq 2.\]

\[y( - 2) = - 2 - 2 = - 4;\]

\[y(2) = 2 + 2 = 4.\]

\[k = \lim_{x \rightarrow + \infty}\frac{f(x)}{x} =\]

\[= \lim_{x \rightarrow + \infty}\left( 1 + \frac{4}{x^{2}} \right) = 1;\]

\[b = \lim_{x \rightarrow + \infty}\left( f(x) - kx \right) =\]

\[= \lim_{x \rightarrow + \infty}\frac{4}{x} = 0;\]

\[x = 0;\text{\ \ \ }\]

\[y = kx + b = x.\]

\[\mathbf{3.}\]

\[\text{\ f}(x) = \frac{x^{2}}{e^{x}};\ \ \ x \in \lbrack - 1;\ 3\rbrack:\]

\[f^{'}(x) = \frac{2x \bullet e^{x} - x^{2} \bullet e^{x}}{e^{2x}} \geq 0;\]

\[e^{x} \bullet \left( 2x - x^{2} \right) \geq 0\]

\[x(2 - x) \geq 0\]

\[x(x - 2) \leq 0\]

\[0 \leq x \leq 2.\]

\[f( - 1) = \frac{1}{e^{- 1}} = e;\]

\[f(0) = \frac{0}{e^{0}} = 0;\]

\[f(2) = \frac{4}{e^{2}};\]

\[f(3) = \frac{9}{e^{3}}.\]

\[Ответ:\ \ e;\ 0.\]

\[\mathbf{4}.\]

\[h - высота\ конуса;\ \]

\[r - радиус\ его\ основания:\]

\[BH = h;\ \ \ AH = r;\text{\ \ \ }\]

\[OH = OE = R;\]

\[OB = h - R;\text{\ \ \ }\]

\[BE = \sqrt{OB^{2} - OE^{2}};\]

\[BE = \sqrt{h^{2} - 2hR + R^{2} - R^{2}} =\]

\[= \sqrt{h^{2} - 2\text{hR}};\]

\[\mathrm{\Delta}ABH\sim\mathrm{\Delta}OBE.\text{\ \ \ \ }\]

\[\frac{\text{OE}}{\text{AH}} = \frac{\text{EB}}{\text{BH}}\]

\[AH = \frac{OE \bullet BH}{\text{EB}} = \frac{R \bullet h}{\sqrt{h^{2} - 2\text{hR}}}.\]

\[V(h) = \frac{1}{3} \bullet \pi \bullet \frac{R^{2}h^{2}}{h^{2} - 2\text{hR}} \bullet h =\]

\[= \frac{\pi R^{2}h^{3}}{3\left( h^{2} - 2\text{hR} \right)};\]

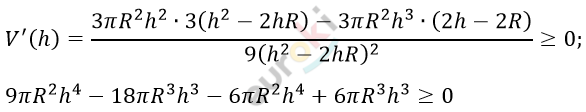
\[3\pi R^{2}h^{4} - 12\pi R^{3}h^{3} \geq 0\]

\[3\pi R^{2}h^{3} \bullet (h - 4R) \geq 0\]

\[h \leq 0;\ \ \ h \geq 4R.\]

\[Точка\ минимума:\]

\[h = 4R.\]

\[Ответ:\ \ 4R.\]